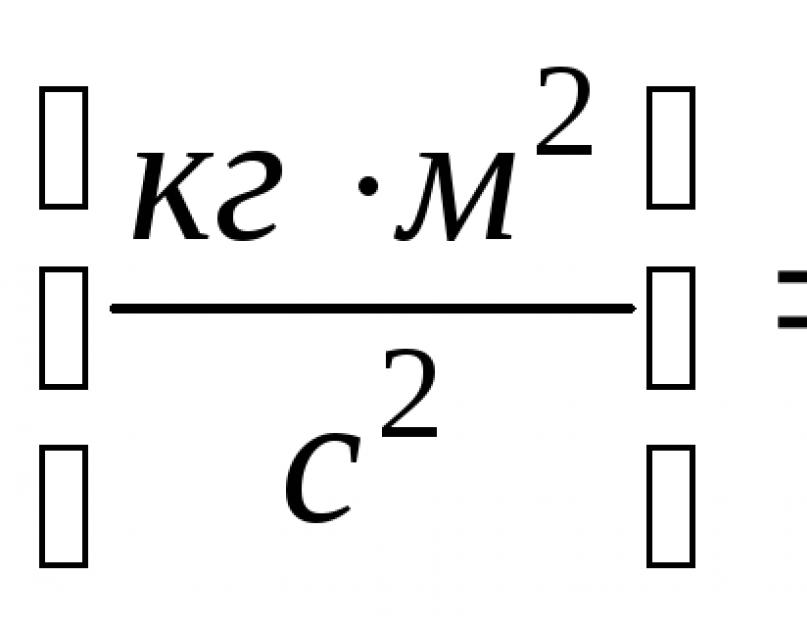Данная теорема устанавливает количественную взаимосвязь между работой силы (причиной) и кинетической энергией материальной точки (следствием).

Кинетической энергией материальной точки называется скалярная величина, равная половине произведения массы точки на квадрат ее скорости

. (43)

Кинетическая энергия характеризует то механическое действие силы, которое может превратиться в другие виды энергии, например, в тепловую.

Работой силы на данном перемещении называется характеристика того действия силы, которое приводит к изменению модуля скорости.

Элементарная работа силы определяется как скалярное произведение вектора силы на элементарный вектор перемещения в точке ее приложения

, (44)

где
- элементарное перемещение.

Модуль элементарной работы определяется формулой

где  - угол между вектором силы и вектором элементарного перемещения; - проекция вектора силы на касательную.

Полная работа на некотором конечном перемещении определяется интегралом

. (46)

Из (46) следует, что полная работа может быть вычислена в двух случаях, когда сила постоянная или зависит то перемещения.

При F =const получаем
.

При решении задач часто удобно пользоваться аналитическим способом вычисления силы

где F x , F y , F z – проекции силы на координатные оси.

Докажем следующую теорему.

Теорема : Изменение кинетической энергии материальной точки на некотором ее перемещении равно работе силы, действующей на точку, на том же перемещении.

Пусть материальная точка M массы m движется под действием силы F из положения M 0 в положение M 1 .

ОУД:
. (47)

Введем подстановку
и спроектируем (47) на касательную

. (48)

Разделяем в (48) переменные и интегрируем

В результате получим

. (49)

Уравнение (49) доказывает сформулированную выше теорему.

Теоремой удобно пользоваться, когда среди заданных и искомых параметров присутствуют масса точки, ее начальная и конечная скорость, силы и перемещение.

Вычисление работы характерных сил.

1. Работа силы тяжести вычисляется как произведение модуля силы на перемещение точки ее приложения по вертикали

. (50)

При перемещении вверх работа положительная, при перемещении вниз – отрицательная.

2. Работа упругой силы пружины F =-cx равна

, (51)

где x 0 – начальное удлинение (сжатие) пружины;

x 1 – конечное удлинение (сжатие) пружины.

Работа силы тяжести и упругой силы не зависят от траектории перемещения их точек приложения. Такие силы, работа которых не зависит от траектории, называются потенциальными силами .

3. Работа силы трения .

Так как сила трения всегда направлена в сторону, противоположную направлению перемещения, то ее работа равна

Работа силы трения всегда отрицательная . Силы работа которых всегда отрицательна, называются диссипативными .

Пример решения задачи с применением теоремы об изменении кинетической энергии системы с твердыми телами, блоками, шкивами и пружиной.

Содержание

Условие задачи

Механическая система состоит из грузов 1 и 2, ступенчатого шкива 3 с радиусами ступеней R 3 = 0,3 м , r 3 = 0,1 м и радиусом инерции относительно оси вращения ρ 3 = 0,2 м , блока 4 радиуса R 4 = 0,2 м и подвижного блока 5. Блок 5 считать сплошным однородным цилиндром. Коэффициент трения груза 2 о плоскость f = 0,1 . Тела системы соединены друг с другом нитями, перекинутыми через блоки и намотанными на шкив 3. Участки нитей параллельны соответствующим плоскостям. К подвижному блоку 5 прикреплена пружина с коэффициентом жесткости с = 280 Н/м .

Под действием силы F = f(s) = 80(6 + 7 s) Н , зависящей от перемещения s точки ее приложения, система приходит в движение из состояния покоя. Деформация пружины в момент начала движения равна нулю. При движении на шкив 3 действует постоянный момент M = 1,6 Н·м сил сопротивления (от трения в подшипниках). Массы тел: m 1 = 0 , m 2 = 5 кг , m 3 = 6 кг , m 4 = 0 , m 5 = 4 кг .

Определить значение центра масс тела 5 V C5 в тот момент времени, когда перемещение s груза 1 станет равным s 1 = 0,2 м .

Указание . При решении задачи использовать теорему об изменении кинетической энергии .

Решение задачи

Дано: R 3 = 0,3 м , r 3 = 0,1 м , ρ 3 = 0,2 м , R 4 = 0,2 м , f = 0,1 , с = 280 Н/м , m 1 = 0 , m 2 = 5 кг , m 3 = 6 кг , m 4 = 0 , m 5 = 4 кг , F = f(s) = 80(6 + 7 s) Н , s 1 = 0,2 м .

Найти: V C5 .

Обозначения переменных

R 3 , r 3 - радиусы ступеней шкива 3;
ρ 3 - радиус инерции шкива 3 относительно оси вращения;
R 5 - радиус блока 5;
V 1 , V 2 - скорости тел 1 и 2;
ω 3 - угловая скорость вращения шкива 3;
V C5 - скорость центра масс C 5 блока 5;
ω 5 - угловая скорость вращения блока 5;
s 1 , s 2 - перемещение тел 1 и 2;
φ 3 - угол поворота шкива 3;
s C5 - перемещение центра масс C 5 блока 5;
s A , s B - перемещение точек A и B.

Установление кинематических соотношений

Установим кинематические соотношения. Поскольку грузы 1 и 2 связаны одной нитью, то их скорости равны:
V 2 = V 1 .
Поскольку нить, соединяющая грузы 1 и 2 намотана на внешнюю ступень шкива 3, то точки внешней ступени шкива 3 движутся со скоростью V 2 = V 1 . Тогда угловая скорость вращения шкива:
.
Скорость центра масс V C5 блока 5 равна скорости точек внутренней ступени шкива 3:
.
Скорость точки K равна нулю. Поэтому она является мгновенным центром скоростей блока 5. Угловая скорость вращения блока 5:
.
Скорость точки B - свободного конца пружины - равна скорости точки A:
.

Выразим скорости через V C5 .
;
;
.

Теперь установим связи между перемещениями тел и углами поворота шкива и блока. Поскольку скорости и угловые скорости являются производными по времени от перемещений и углов поворота
,
то такие же связи будут между перемещениями и углами поворота:
s 2 = s 1 ;
;
;
.

Определение кинетической энергии системы

Найдем кинетическую энергию системы. Груз 2 совершает поступательное движение со скоростью V 2 . Шкив 3 совершает вращательное движение с угловой скоростью вращения ω 3 . Блок 5 совершает плоскопараллельное движение. Он вращается с угловой скоростью ω 5 и его центр масс движется со скоростью V C5 . Кинетическая энергия системы:
.

Поскольку радиус инерции шкива относительно оси вращения задан, то момент инерции шкива относительно оси вращения определяется по формуле:
J 3 = m 3 ρ 2 3 .
Поскольку блок 5 является сплошным однородным цилиндром, то его момент инерции относительно центра масс равен
.

С помощью кинематических соотношений выражаем все скорости через V C5 и подставляем выражения для моментов инерции в формулу для кинетической энергии.
,
где мы ввели постоянную
кг.

Итак, мы нашли зависимость кинетической энергии системы от скорости центра масс V C5 подвижного блока:
, где m = 75 кг.

Определение суммы работ внешних сил

Рассмотрим внешние силы , действующие на систему.
При этом мы не рассматриваем силы натяжения нитей, поскольку нити нерастяжимые и, поэтому, они не производят работу. По этой причине мы не рассматриваем внутренние напряжения, действующие в телах, поскольку они являются абсолютно твердыми.
На тело 1 (с нулевой массой) действует заданная сила F .
На груз 2 действует сила тяжести P 2 = m 2 g 2 и сила трения F T .
На шкив 3 действует сила тяжести P 3 = m 3 g , сила давления оси N 3 и момент сил трения M .
На шкив 4 (с нулевой массой) действует сила давления оси N 4 .
На подвижный блок 5 действует сила тяжести P 5 = m 5 g , сила упругости F y пружины и сила натяжения нити T K в точке K .

Работа, которую совершает сила при перемещении точки ее приложения на малое смещение равна скалярному произведению векторов , то есть произведению модулей векторов F и ds на косинус угла между ними. Заданная сила , приложенная к телу 1, параллельна перемещению тела 1. Поэтому работа, которую совершает сила , при перемещении тела 1 на расстояние s 1 равна:


Дж.

Рассмотрим груз 2. На него действуют сила тяжести P 2 , сила давления поверхности N 2 , силы натяжения нитей T 23 , T 24 и сила трения F T . Поскольку груз не совершает перемещения в вертикальном направлении, то проекция его ускорения на вертикальную ось равна нулю. Поэтому сумма проекций сил на вертикальную ось равна нулю:
N 2 - P 2 = 0 ;
N 2 = P 2 = m 2 g .
Сила трения:
F T = f N 2 = f m 2 g .
Силы P 2 и N 2 перпендикулярны перемещению s 2 , поэтому они работу не производят.
Работа силы трения:
Дж.

Если рассматривать груз 2 как изолированную систему, то нужно учитывать работу, произведенную силами натяжения нитей T 23 и T 24 . Однако нас интересует вся система, состоящая из тел 1, 2, 3, 4 и 5. Для такой системы силы натяжения нитей являются внутренними силами. А поскольку нити нерастяжимые, то сумма их работ равна нулю. В случае с грузом 2, нужно еще учесть силы натяжения нитей, действующих на шкив 3 и блок 4. Они равны по величине и противоположны по направлению силам T 23 и T 24 . Поэтому работа, производимая силами натяжения нитей 23 и 24 над грузом 2 равна по величине и противоположна по знаку работе, производимой силами натяжения этих нитей над шкивом 3 и блоком 4. В результате сумма работ, производимая силами натяжения нитей равна нулю.

Рассмотрим шкив 3. Поскольку его центр масс не перемещается, то работа силы тяжести P 3 равна нулю.
Поскольку ось C 3 неподвижна, то сила давления оси N 3 работу не производит.
Работа, произведенная моментом сил , вычисляется аналогично работе, произведенной силой :
.
В нашем случае, векторы момента сил трения и угла поворота шкива направлены вдоль оси вращения шкива, но противоположны по направлению. Поэтому работа момента сил трения:
Дж.

Рассмотрим блок 5.
Поскольку скорость точки K равна нулю, то сила T K работу не производит.
Центр масс блока C 5 переместился на расстояние s C5 вверх. Поэтому работа силы тяжести блока равна:
Дж.
Работа силы упругости пружины равна изменению потенциальной энергии пружины со знаком минус. Поскольку вначале пружина не деформирована, то
Дж.

Сумма работ всех сил:

Дж.

Применение теоремы об изменении кинетической энергии системы

Применим теорему об изменении кинетической энергии системы в интегральной форме.
.
Поскольку в начале система покоилась, то ее кинетическая энергия в начале движения
T 0 = 0 .
Тогда
.
Отсюда
м/с.

Лекция 5. Теорема об изменении кинетической энергии

5. 1. Работа силы

Пусть сила – равнодействующая всех сил системы, приложена к точке Р, а (dx , dy , dz ) – элементарное перемещение точки Р вдоль ее траектории Р 1 Р 2 (рис. 5.1). Элементарной работой d А силы называют скалярное произведение

Элементарная работа является скалярной величиной. Если - угол между силой и направлением перемещения , то выражение (5.1) можно представить в виде

где - проекция силы на направление элементарного перемещения (или направление скорости точки).

Знак элементарной работы зависит от знака функции . Если - острый угол, то , если - тупой угол, то , если , то .

Пусть точка Р совершает конечное перемещение из положения в положение , описывая дугу . Разобьем дугу на n произвольных малых участков, обозначив длину участка с номером k через . Тогда элементарная работа силы на k -м участке будет равна , а на всем пути от до - сумме работ на отдельных участках

Точное значение работы получим, переходя к пределу, при условии, что число участков n неограниченно возрастает, а длина каждого участка убывает:

.

Такой предел называется криволинейным интегралом первого рода по дуге и записывается следующим образом

. (5.3)

Результат интегрирования является полной работой А силы F на рассматриваемом конечном перемещении вдоль пути .

5. 1. 1. Работа силы тяжести

Пусть m – масса точки, g – ускорение свободного падения. Тогда

Вычисляя работу по формулам (5.1) и (5.3), имеем

где - высота опускания точки.

При подъеме точки , следовательно, .

5. 1. 2. Работа линейной силы упругости

Пусть материальная точка Р движется вдоль оси Ох (рис. 5.3) под действием пружины, к которой она прикреплена. Если при , , то пружина деформирована и при малых отклонениях точки можно считать, что со стороны пружины к ней приложена сила упругости . Тогда работа силы упругости на перемещении x 0 x 1 будет равна

. (5.5)

Работа силы упругости равна половине произведения коэффициента жесткости на разность квадратов начального и конечного удлинения (или сжатий) пружины.

5. 1. 3. Элементарная работа сил, приложенных к твердому телу

Рассмотрим движение тела в плоскости. Пусть О – произвольно выбранная точка на твердом теле (рис.5.4). Назовем ее полюсом. Тогда движение тела в плоскости можно представить как сумму простейших: поступательного движения вместе с полюсом и вращение тела вокруг полюса. Тогда, скорость точки относительно неподвижной системы координат определится как геометрическая сумма двух скоростей

где - скорость полюса, - вектор угловой скорости твердого тела, – скорость Эйлера, т е. скорость точки при ее ращении вокруг полюса.

Будем представлять твердое тело как механическую систему, состоящую из N отдельных точек, взаимное расстояние между которыми не изменяется.

Вычислим смещение точки под действием силы :

Тогда .

Элементарная работа, согласно (5.1), запишется следующим образом

Воспользовавшись свойствами смешенного произведения векторов , перепишем последнее выражение в виде

Пусть - равнодействующая всех сил, внешних и внутренних (рис5.4), приложенных в точке тела, т.е.

.

Тогда (а) запишется так

Согласно (3.1 и 3.2), главный вектор и главный момент внутренних сил системы равны нулю, получаем

здесь: – главный вектор, – главный момент внешних сил относительно точки О .

Частные случаи

A. Поступательное движение твердого тела . Все точки тела имеют одинаковые перемещения (рис. 5.5, а) и по модулю, и по направлению, тогда, из (5.6), получим (здесь ):

. (5.7)

B. Вращение твердого тела вокруг неподвижной оси . Пусть ось z проходит через полюс О (рис. 5.5б). Тогда , ; из (5.6) получим

. (5.8)

Пример. Катушка массой m и радиусом R приводится в движение постоянной силой F , приложенной в точке А (рис. 5.6). Катушка катится вправо без скольжения по шероховатой поверхности.

Вычислить работу всех внешних сил, если центр катушки переместился на расстояние , - коэффициент трения качения, - сила трения, r – радиус сердечника катушки, к которой приложена сила.

Решение. Катушка совершает плоское движение. Так как качение происходит без скольжения, то мгновенный центр скоростей находится в точке касания катушки с плоскостью, т.е. в точке Р (рис.5.6). Направим ось S по горизонтали вправо. В соответствии с направлением движения примем положительное направление угла поворота против хода часовой стрелки.

Пусть центр катушки С переместится на . При этом катушка повернется на угол . Тогда , откуда

Приняв точку Р за мгновенную ось вращения, вычислим элементарную работу по формуле (5.8):

(а)

Здесь: линии действия сил и mg пересекают ось вращения, поэтому ; далее , где N – сила нормальной реакции.

Для определения искомой работы остается взять определенный интеграл от (а) в пределах от 0 до S А . Получим

5. 2. Силовое поле. Силовая функция. Потенциальная энергия

Предположим, что точка движется в некотором пространстве и на нее со стороны пространства действует сила, которая зависит от положения точки в этом пространстве, но не зависит от скорости движения точки. В этом случае говорят, что в пространстве задано силовое поле , а также, что точка движется в силовом поле. Соответствующие понятия для системы материальных точек аналогичны.

Силы, зависящие от положения точек их приложения, в механике встречаются часто. Например, сила упругости, приложенная к материальной точке, которая движется по горизонтальной прямой под действием пружины. Важнейшим примером силового поля в природе является гравитационное поле: действие Солнца на планету данной массы определяется в каждой точке пространства законом всемирного тяготения.

Силовое поле называется потенциальным , если существует скалярная функция U , зависящая только от координат , , точки -точки материальной системы (возможно, и от времени), такая, что

Функция называется силовой функцией .

Рассмотрим свойства силовой функции.

Элементарная работа (5.1) связана с силовой функцией следующим образом

Таким образом, элементарная работа силы в потенциальном силовом поле равна полному дифференциалу от силовой функц ии.

Полная работа силы на участке от точки до точки (рис.5.1)

т.е. . (5.10)

Из полученных выражений следует, что

1. работа силы в потенциальном силовом поле по любому замкнутому пути равна нулю;

2. работа силы в потенциальном силовом поле зависит только от положения конечной и начальной точек, но сам путь перемещения роли не играет.

Потенциальная энергия. Потенциальной энергией П в рассматриваемой точке силового поля Р называют работу, которую совершают силы поля, действующую на материальную точку при ее перемещении из точки Р в начальную точку 1 , т.е.

П = или П =

Свяжем силовую функцию U с потенциальной энергией. Имеем

Примеры вычисления потенциальной энергии

1. Однородное поле тяжести . Пусть m – масса точки; g – ускорение свободного падения. Тогда (рис. 5.2)

2. Силовое поле упругой пружины . Пусть материальная точка движется вдоль оси Ох (рис. 5.3) под действием пружины, к которой она прикреплена. Если при пружина не деформирована, то, полагая в формуле (5.5) , получим

.

5. 3. Кинетическая энергия

5. 3. 1. Кинетическая энергия системы. Теорема Кенига

Кинетической энергией материальной точки называют половину произведения массы точки на квадрат ее скорости, т.е. . Кинетическая энергия, является скалярной положительной величиной. В системе СИ, единицей измерения кинетической энергии является джоуль: .

Кинетической энергией механической системы называется сумма кинетических энергий всех точек, входящих в систему:

(5.11)

Скорости точек системы (5.1) определяются относительно неподвижной системы отсчета.

Совместим начало координат с центром масс системы. Предположим, что механическая система вместе с системой координат движется поступательно относительно неподвижной системы координат (рис.5.7). Точка – точка системы.

Тогда, на основании теоремы о сложении скоростей, абсолютная скорость точки Р k . системы запишется так векторная сумма переносной и относительной скоростей:

, (а)

где – скорость начала подвижной системы координат (переносная скорость, т.е. скорость центра масс системы); – скорость точки Р k относительно подвижной системы координат Оху z (относительная скорость).

Подставляя (а) в формулу (5.11), получаем

(5.12)

Здесь - масса всей системы.

Радиус-вектор центра масс системы в подвижной системе координат определяется, согласно (2.1), – , откуда , т.е. . Поскольку начало координат О является центром масс системы, то , тогда , т.е. вторая сумма в выражении (5.12) равна нулю.

Таким образом, кинетическая энергия системы (5.12) имеет вид

(5.13)

Это равенство определяет теорему Кенига.

Теорема . Кинетическая энергия системы равна сумме кинетической энергии, которую имела бы материальная точка, расположенная в центре масс системы и имеющая массу, равную массе системы, и кинетической энергии движения системы относительно центра масс.

5. 3. 2. Кинетическая энергия твердого тела

Твердое тело является частным случаем механической системы и рассматривается как непрерывно распределенная масса, тогда все суммы, входящие в выражение для кинетической энергии системы, переходят в интегралы. Так, для твердого тела формула (5.11) примет вид

. (5.14)

1. Кинетическая энергия твердого тела, двигающегося поступательно.

При этом виде движения скорости всех точек тела одинаковы (рис. 5.8). Вынося в формуле (5.14) за знак интеграла, получим

. (5.15)

Кинетическая энергия твердого тела, движущегося поступательно, равна половине произведения массы тела M на квадрат его скорости.

2. Кинетическая энергия твердого тела, вращающегося вокруг неподвижной оси

Модуль скорости V любой точки твердого тела, вращающегося вокруг неподвижной оси, равен , где - модуль угловой скорости твердого тела, - расстояние от точки до оси вращения z (рис. 5.9). Подставляя в формулу (5.14), получим

здесь – момент инерции твердого тела относительно оси z .

Кинетическая энергия твердого тела, вращающегося вокруг неподвижной оси, равна половине произведения момента инерции тела относительно оси вращения на квадрат угловой скорости тела.

3. Кинетическая энергия твердого тела при плоско – параллельном движении

При плоско – параллельном движении скорость любой точки тела состоит из геометрической суммы скорости полюса и скорости точки при вращении вокруг полюса. Пусть тело движется плоско в плоскости Oxy , тогда

|| . За полюс выбираем центр масс тела, тогда в формуле (5.13), скорость есть скорость точки k тела при ее вращении относительно полюса (центра масс) и равна , где расстояние k - ой точки до полюса. Тогда (5.13) перепишется

Имея в виду, что – момент инерции тела относительно оси z , проходящей через полюс С , последнее выражение можно переписать как

, (5.17)

при плоско – параллельном движении тела кинетическая энергия складывается из кинетической энергии поступательного движения вместе с центром масс и кинетической энергии от вращения вокруг оси, проходящей через центр масс и перпендикулярной плоскости движения.

5. 4. Теорема об изменении кинетической энергии

5. 4. 1. Теорема об изменении кинетической энергии точки

Найдем связь между работой и изменением скорости. Пусть материальная точка массой m перемещается вдоль оси Ох под действием силы, например сжатой или разжатой пружины, закрепленной в начале координат, – точке О (рис. 5.10). Уравнение движения точки имеет вид

Умножим обе части этого уравнения на , и, учитывая, что , получим

. (5.19)

В правой части этого равенства заменим V x на и умножим на dt правую и левую части. Тогда

. (5.20)

В этом виде равенство имеет очень наглядный смысл: при смещении точки на dx , сила совершает работу , в результате чего изменяется величина кинетической энергии точки , характеризующая движение точки и, в частности, модуль ее скорости. Если точка смещается из положения в , а ее скорость при этом изменяется от до , то, интегрируя (5.20), имеем

. (5.21)

Учитывая, что , окончательно находим

. (5.22)

Изменение кинетической энергии материальной точки при ее каком-либо перемещении равно работе силы, действующей на точку на том же перемещении.

Проделывая все предыдущие процедуры, получим

,

здесь – дуга, вдоль которой перемещается точка (рис. 5.11).

5. 4. 2. Теорема об изменении кинетической энергии системы

Пусть точки системы массой переместились так, что их радиус-векторы в инерциальной системе отсчета получили приращение . Найдем, как при этом изменилась кинетическая энергия Т системы.

Согласно (5.11), кинетическая энергия системы

.

Вычислим дифференциал кинетической энергии системы и преобразуем полученное выражение

здесь

Принимая во внимание, что , где - ускорение точки а и - равнодействующие внешних и внутренних сил, приложенных к точке, перепишем последнее равенство в виде

Таким образом,

. (5.23)

Последнее равенство выражает теорему об изменении кинетической энергии механической системы в дифференциальной форме: дифференциал кинетической энергии системы равен элементарной работе всех сил системы.

Частный случай . Для абсолютно твердого тела сумма работ всех внутренних сил системы равна нулю:

.

Следовательно, теорему об изменении кинетической энергии (5.23) для твердого тела можно записать в виде

Изменение кинетической энергии твердого тела при каком-либо элементарном перемещении равно элементарной работе внешних сил, действующих на тело.

Если обе части (5.24) проинтегрировать между двумя положениями – начальным и конечным, в которых соответственно кинетическая энергия и , получаем

. (5.25)

Пример 1 . Диск массой m =5 кг и радиусом приводится в движение постоянной силой , приложенной в точке А (рис. 5.6). Диск катится по шероховатой поверхности вправо без скольжения. Определить скорость центра масс С катушки в момент, когда он переместится на расстояние , коэффициент трения скольжения , , радиус инерции диска

Решение. Диск совершает плоское движение. Запишем теорему об изменении кинетической энергии для твердого тела

Вычислим кинетическую энергию диска. В начальный момент времени диск находился в покое, т.е. . Кинетическая энергия в конечном положении диска

Просмотр: эта статья прочитана 49915 раз

Pdf Выберите язык... Русский Украинский Английский

Краткий обзор

Полностью материал скачивается выше, предварительно выбрав язык

Два случая преобразования механического движения материальной точки или системы точек:

1. механическое движение переносится с одной механической системы на другую в качестве механического движения;
2. механическое движение превращается в другую форму движения материи (в форму потенциальной энергии, теплоту, электричество и т.д.).

Когда рассматривается преобразование механического движения без перехода его в другую форму движения, мерой механического движения является вектор количества движения материальной точки или механической системы. Мерой действия силы в этом случае является вектор импульса силы.

Когда механическое движение превращается в другую форму движения материи, в качестве меры механического движения выступает кинетическая энергия материальной точки или механической системы. Мерой действия силы при превращении механического движения в другую форму движения является работа силы

Кинетическая энергия

Кинетическая энергия это способность тела преодолевать препятствование во время движения.

Кинетическая энергия материальной точки

Кинетической энергией материальной точки называется скалярная величина, которая равняется половине произведения массы точки на квадрат ее скорости.

Кинетическая энергия:

• характеризует и поступательное, и вращательное движения;
• не зависит от направления движения точек системы и не характеризует изменение этих направлений;
• характеризует действие и внутренних, и внешних сил.

Кинетическая энергия механической системы

Кинетическая энергия системы равняется сумме кинетических энергий тел системы. Кинетическая энергия зависит от вида движения тел системы.

Определение кинетической энергии твердого тела при разных видах движения движениях.

Кинетическая энергия поступательного движения
При поступательном движении кинетическая энергия тела равна Т =m V 2 /2.

Мерой инертности тела при поступательном движении является масса.

Кинетическая энергия вращательного движения тела

При вращательном движении тела кинетическая энергия равняется половине произведения момента инерции тела относительно оси вращения и квадрата его угловой скорости.

Мерой инертности тела при вращательном движении является момент инерции.

Кинетическая энергия тела не зависит от направления вращения тела.

Кинетическая энергия плоскопаралельного движения тела

При плоскопаралельном движении тела кинетическая энергия равна

Работа силы

Работа силы характеризует действие силы на тело при некотором перемещении и определяет изменение модуля скорости подвижной точки.

Элементарная работа силы

Элементарная работа силы определяется как скалярная величина, равная произведению проекции силы на касательную к траектории, направленную в направлении движения точки, и бесконечно малого перемещения точки, направленного вдоль этой касательной.

Работа силы на конечном перемещении

Работа силы на конечном перемещении равна сумме ее работ на элементарных участках.

Работа силы на конечном перемещении М 1 М 0 равняется интегралу вдоль этого перемещения от элементарной работы.

Работа силы на перемещении М 1 М 2 изображается площадью фигуры, ограниченной осью абсцисс, кривой и ординатами, соответствующими точкам М 1 и М 0 .

Единица измерения работы силы и кинетической энергии в системе СИ 1 (Дж).

Теоремы о работе силы

Теорема 1 . Работа равнодействующей силы на некотором перемещении равна алгебраической сумме работ составляющих сил на том же перемещении.

Теорема 2. Работа постоянной силы на результирующем перемещении равна алгебраической сумме работ этой силы на составляющих перемещениях.

Мощность

Мощность - это величина, которая определяет работу силы за единицу времени.

Единицей измерения мощности есть 1Вт = 1 Дж/с.

Случаи определения работы сил

Работа внутренних сил

Сумма работ внутренних сил твердого тела на любом его перемещении равна нулю.

Работа силы тяжести

Работа силы упругости

Работа силы трения

Работа сил, приложенных к вращающемуся телу

Элементарная работа сил, приложенных к твердому телу, вращающемуся вокруг неподвижной оси, равна произведению главного момента внешних сил относительно оси вращения на приращение угла поворота.

Сопротивление качению

В зоне контакта неподвижого цилиндра и плоскости возникает местная деформация контактного сжатия, напряжение распределяются по эллиптическому закону и линия действия равнодействующей N этих напряжений совпадает с линией действия силы нагрузки на цилиндр Q. При перекатывании цилиндра распределение нагрузки становится несимметричным с максимумом, смещенным в сторону движения. Равнодействующая N смещается на величину k - плечо силы трения качения, которая еще назвается коэффициентом трения качения и имеет размерность длины (см)

Теорема об изменении кинетической энергии материальной точки

Изменение кинетической энергии материальной точки на некотором ее перемещении равняется алгебраической сумме робот всех действующих на точку сил на том же перемещении.

Теорема об изменении кинетической энергии механической системы

Изменение кинетической энергии механической системы на некотором перемещении равняется алгебраической сумме робот внутренних и внешних сил, действующих на материальные точки системы на том же перемещении.

Теорема об изменении кинетической энергии твердого тела

Изменение кинетической энергии твердого тела (неизменной системы) на некотором перемещении равняется сумме робот внешних сил, действующих на точки системы на том же перемещении.

КПД

Силы, действующие в механизмах

Силы и пары сил (моменты), которые приложены к механизму или машине, можно разделить на группы:

1.Движущие силы и моменты, совершающие положительную работу (приложенные к ведущим звеньям, например, давление газа на поршень в ДВС).

2. Силы и моменты сопротивления, совершающие отрицательную работу:

• полезного сопротивления (совершают требуемую от машины работу и приложены к ведомым звеньям, например сопротивление поднимаемого машиной груза),
• силы сопротивления (например, силы трения, сопротивление воздуха и т.п.).

3. Силы тяжести и силы упругости пружин (как положительная, так и отрицательная работа, при этом работа за полный цикл равна нулю).

4. Силы и моменты, приложенные к корпусу или стойке извне (реакция фундамента и т.п.), которые не совершают работу.

5. Силы взаимодействия между звеньями, действующие в кинематических парах.

6. Силы инерции звеньев, обусловленные массой и движением звеньев с ускорением, могут осуществлять положительную, отрицательную работу и не совершать работы.

Работа сил в механизмах

При установившемся режиме работы машины ее кинетическая энергия не изменяется и сумма работ приложенных к ней движущих сил и сил сопротивления равна нулю.

Работа, затрачиваемая на приведение машины в движение, расходуется на преодоление полезных и вредных сопротивлений.

КПД механизмов

Механический коэффициент полезного действия при установившемся движении равен отношению полезной работы машины к работе, затраченной на приведение машины в движение:

Элементы машины могут соединяться последовательно, параллельно и смешанно.

КПД при последовательном соединении

При последовательном соединении механизмов общий КПД меньше с наименьшего КПД отдельного механизма.

КПД при параллельном соединении

При параллельном соединении механизмов общий КПД больше наименьшего и меньше наибольшего КПД отдельного механизма.

Формат: pdf

Язык: русский, украинский

Пример расчета прямозубой цилиндрической передачи
Пример расчета прямозубой цилиндрической передачи. Выполнен выбор материала, расчет допускаемых напряжений, расчет на контактную и изгибную прочность.

Пример решения задачи на изгиб балки
В примере построены эпюры поперечных сил и изгибающих моментов, найдено опасное сечение и подобран двутавр. В задаче проанализировано построение эпюр с помощью дифференциальных зависимостей, провелен сравнительный анализ различных поперечных сечений балки.

Пример решения задачи на кручение вала
Задача состоит в проверке прочности стального вала при заданном диаметре, материале и допускаемых напряжениях. В ходе решения строятся эпюры крутящих моментов, касательных напряжений и углов закручивания. Собственный вес вала не учитывается

Пример решения задачи на растяжение-сжатие стержня
Задача состоит в проверке прочности стального стержня при заданных допускаемых напряжениях. В ходе решения строятся эпюры продольных сил, нормальных напряжений и перемещений. Собственный вес стержня не учитывается

Применение теоремы о сохранении кинетической энергии
Пример решения задачи на применение теоремы о сохранение кинетической энергии механической системы

Кинетическая энергия механической системы - это сумма кинетических энергий всех ее материальных точек:

Вычислим дифференциал от выражения кинетической энергии и выполним некоторые простые преобразования:

Опуская промежуточные значения и применяя ранее введенный для обозначения элементарной работы символ , запишем:

Итак, дифференциал кинетической энергии механической системы равен сумме элементарных работ всех внешних и внутренних сил, действующих на точки системы. В этом и состоит содержание теоремы об изменении кинетической энергии.

Заметим, что сумма работ внутренних сил системы в общем случае не равна нулю. Она обращается в нуль только в некоторых частных случаях: когда системой служит абсолютно твердое тело; система абсолютно твердых тел, взаимодействующих при помощи не-деформируемых элементов (идеальных шарниров, абсолютно твердых стержней, нерастяжимых нитей и т.п.). По этой причине теорема об изменении кинетической энергии является единственной из общих теорем динамики, которая учитывает эффект действия внутренних сил.

Можно интересоваться изменением кинетической энергии не за бесконечно малый промежуток времени, как это делается выше, а за некоторый конечный промежуток времени . Тогда при помощи интегрирования можно получить:

Здесь - значения кинетической энергии соответственно в моменты времени - суммы полных работ внешних и внутренних сил за рассматриваемый промежуток времени.

Полученное равенство выражает теорему об изменении кинетической энергии в конечной (интегральной) форме, которая может быть сформулирована так: изменение кинетической энергии при переходе механической системы из одного положения в другое равно сумме полных работ всех внешних и внутренних сил.