Проекции скоростей двух точек твердого тела на ось, проходящую через эти точки, равны друг другу.
v A cos α = v B cos β .

Доказательство

Выберем прямоугольную неподвижную систему координат Oxyz . Возьмем две произвольные точки твердого тела A и B . Пусть (x A , y A , z A ) и (x B , y B , z B ) - координаты этих точек. При движении твердого тела они являются функциями от времени t . Дифференцируя по времени, получаем проекции скоростей точек.
, .

Воспользуемся тем, что при движении твердого тела, расстояние | AB| между точками остается постоянным, то есть не зависит от времени t . Также постоянным является квадрат расстояния
.
Продифференцируем это уравнение по времени t , применяя правило дифференцирования сложной функции.

Сократим на 2 .
(1)

Введем вектор
.
Тогда уравнение (1) можно представить в виде скалярного произведения векторов.
(2)
Выполняем преобразования.
;
(3) .
По свойству скалярного произведения
,
.
Подставляем в (3) и сокращаем на | AB| .
;

Что и требовалось доказать.

Относительная скорость

Рассмотрим движение точки B относительно точки A . Введем относительную скорость точки B относительно A .

Тогда уравнение (2) можно переписать в виде
.

То есть относительная скорость перпендикулярна вектору , проведенному из точки A в точку B . Поскольку точка B взята произвольным образом, то относительная скорость любой точки твердого тела перпендикулярна радиус вектору, проведенному из точки A . То есть относительно точки A тело совершает вращательное движение. Относительная скорость точек тела определяется по формуле для вращательного движения
.

Точку A , относительно которой рассматривают движение, часто называют полюсом .

Абсолютную скорость точки B относительно неподвижной системы координат можно записать в следующем виде:
.
Она равна сумме скорости поступательного движения произвольной точки A (полюса) и скорости вращательного движения относительно полюса A .

Пример решения задачи

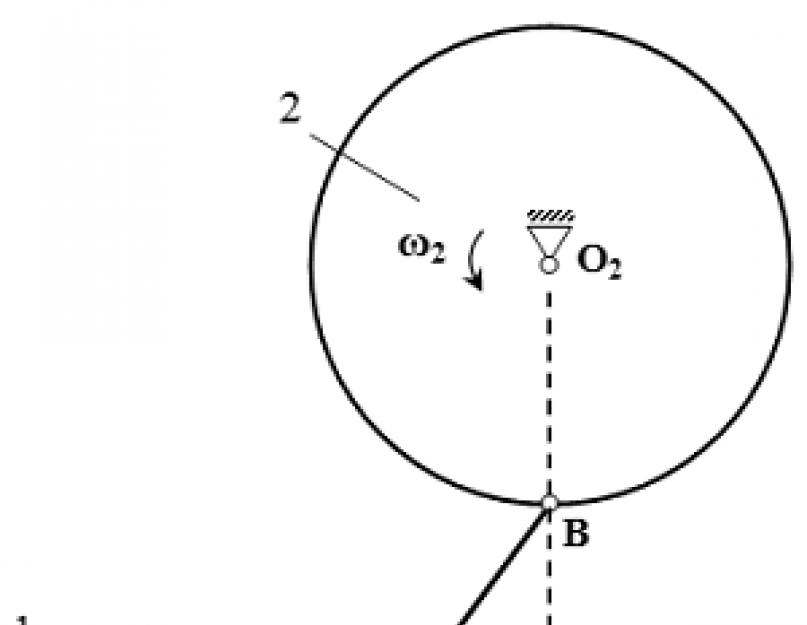
Условие задачи

Колеса 1 и 2 с радиусами R 1 = 0,15 м и R 2 = 0,3 м , соответственно, соединены шарнирами со стержнем 3 длины | AB| = 0,5 м . Колесо 1 вращается с угловой скоростью ω 1 = 1 рад/с . Для изображенного на рисунке положения механизма, определить угловую скорость ω 2 колеса 2. Принять L = 0,3 м .

Решение задачи

Точка A движется по окружности радиуса R 1 вокруг центра вращения O 1 . Скорость точки A определяется по формуле
V A = ω 1 R 1 .
Вектор направлен вертикально (перпендикулярно O 1 A ).

Точка B движется по окружности радиуса R 2 вокруг центра вращения O 2 . Скорость точки B определяется по формуле
V B = ω 2 R 2 .
Отсюда
.
Вектор направлен горизонтально (перпендикулярно O 2 B ).

Строим прямоугольный треугольник ABC . Применяем теорему Пифагора.
(м)
.
Косинус угла между вектором скорости и прямой AB , в направлении вектора , равен
.

По теореме о проекциях скоростей двух точек твердого тела на прямую имеем:
V A cos α = V B cos β .
Отсюда
.

Находим угловую скорость колеса 2 .
рад/с .

1.2. Прямолинейное движение

1.2.3. Графическое вычисление кинематических величин

Некоторые кинематические характеристики движения можно рассчитать графическим способом.

Определение проекции скорости

По графикам зависимости координаты от времени x (t ) (или пройденного пути от времени S (t )) можно рассчитать соответствующую проекцию скорости v x в определенный момент времени (рис. 1.11), например t = t 1 .

Для этого следует:

1) отметить на оси времени указанное значение момента времени t 1 ;

2) восстановить перпендикуляр до пересечения с графиком x (t );

5) определить проекцию скорости на ось Ox как тангенс угла наклона касательной к положительному направлению оси времени:

v x (t 1) = tg α 1 .

Следует отметить, что проекция скорости v x является

• положительной , если касательная к графику образует острый угол с направлением оси t (см. рис. 1.11);
• отрицательной , если касательная к графику образует тупой угол с направлением оси t (рис. 1.12).

На рис. 1.12 изображен график зависимости координаты от времени x (t ). Для определения проекции скорости на ось Ox в момент времени t 3 проведен перпендикуляр t = t 3 . В точке пересечения перпендикуляра с зависимостью x (t ) проведена касательная линия. Она образует тупой угол с осью t . Следовательно, проекция скорости v x на ось Ox в указанный момент времени является отрицательной величиной:

v x (t 3) = − | tg α 3 | .

Рис. 1.12

Определение проекции ускорения

По графику зависимости проекции скорости от времени v x (t ) можно рассчитать проекцию ускорения a x на соответствующую ось в определенный момент времени (рис. 1.13), например t = t 2 .

Для этого следует:

1) отметить на оси времени указанное значение момента времени t 2 ;

2) восстановить перпендикуляр до пересечения с графиком v x (t );

3) провести к графику касательную линию в точке его пересечения с перпендикуляром;

5) определить проекцию ускорения на ось Ox как тангенс угла наклона касательной к положительному направлению оси времени:

a x (t 2) = tg α 2 .

Следует отметить, что проекция ускорения a x является

• положительной , если касательная к графику образует острый угол с направлением оси t (см. рис. 1.13);

Рис. 1.13

• отрицательной , если касательная к графику образует тупой угол с направлением оси t (рис. 1.14).

Рис. 1.14

Пояснение к использованию алгоритма. На рис. 1.14 изображен график зависимости проекции скорости от времени v x (t ). Для определения проекции ускорения на ось Ox в момент времени t 4 проведен перпендикуляр t = t 4 . В точке пересечения перпендикуляра с зависимостью v x (t ) проведена касательная линия. Она образует тупой угол с осью t . Следовательно, проекция ускорения a x на ось Ox в указанный момент времени является отрицательной величиной:

a x (t 4) = − | tg α 4 | .

Определение пройденного пути и модуля перемещения (комбинация равномерного и равноускоренного движения)

По графику зависимости проекции скорости от времени v x (t ) можно рассчитать пройденный путь и модуль перемещения материальной точки (тела) за определенный промежуток времени ∆t = t 2 − t 1 .

Для расчета указанных характеристик по графику, содержащему участки только равноускоренного и равномерного движения, следует:

4) вычислить пройденный путь S и модуль перемещения ∆r как суммы:

∆r = S 1 + S 2 + ... + S n ,

где S 1 , S 2 , ..., S n - пути, пройденные материальной точкой на каждом из участков равноускоренного и равномерного движения.

На рис. 1.15 показана зависимость проекции скорости от времени для материальной точки (тела), движущейся на участке AB равноускоренно, на участке BC - равномерно, на участке CD - равноускоренно, но с ускорением, отличающимся от ускорения на участке AB .

Рис. 1.15

В этом случае пройденный путь S и модуль перемещения ∆r совпадают и рассчитываются по формулам:

S = S 1 + S 2 + S 3 ,

∆r = S 1 + S 2 + S 3 ,

где S 1 - путь, пройденный материальной точкой (телом) на участке AB ; S 2 - путь, пройденный на участке BC ; S 3 - путь, пройденный на участке CD ; S 1 , S 2 , S 3 рассчитываются по алгоритму, приведенному выше.

Определение пройденного пути и модуля перемещения (комбинация равномерного, равноускоренного и равнозамедленного движения)

Для расчета указанных характеристик по графику v x (t ), содержащему участки не только равноускоренного и равномерного, но и равнозамедленного движения, следует:

1) отметить на оси времени указанный интервал времени ∆t ;

2) восстановить перпендикуляры из точек t = t 1 и t = t 2 до пересечения с графиком v x (t );

4) вычислить пройденный путь S как сумму:

S = S 1 + S 2 + ... + S n ,

где S 1 , S 2 , ..., S n - пути, пройденные материальной точкой на каждом из участков;

5) вычислить модуль перемещения как разность суммарного пути, пройденного материальной точкой до точки остановки, и пути, пройденного материальной точкой после остановки.

Пояснение к использованию алгоритма . На рис. 1.16 показана зависимость скорости от времени для материальной точки (тела), движущейся на участке AB равноускоренно, на участке BC - равномерно, на участке CF - равнозамедленно.

Рис. 1.16

В том случае, когда есть участок равнозамедленного движения (включающий точку остановки - точка D ), пройденный путь S и модуль перемещения ∆r не совпадают. Пройденный путь вычисляют по формуле

S = S 1 + S 2 + S 3 + S 4 ,

где S 1 - путь, пройденный материальной точкой (телом) на участке AB ; S 2 - путь, пройденный на участке BC ; S 3 - путь, пройденный на участке CD ; S 4 - путь, пройденный на участке DF ; S 1 , S 2 , S 3 , S 4 рассчитываются по алгоритму, приведенному выше; необходимо отметить, что величина S 4 является положительной.

Модуль перемещения вычисляют по формуле

∆r = S 1 + S 2 + S 3 − S 4 ,

вычитая путь, пройденный материальной точкой (телом) после поворота.

Определение модуля изменения скорости

По графику зависимости проекции ускорения от времени a x (t ) можно найти модуль изменения скорости ∆v материальной точки (тела) за определенный интервал времени ∆t = t 2 − t 1 (рис. 1.17).

Для этого следует:

1) отметить на оси времени указанный интервал времени ∆t ;

2) восстановить перпендикуляры из точек t = t 1 и t = t 2 до пересечения с графиком a x (t );

4) вычислить модуль изменения скорости за указанный интервал времени как площадь.

Пример 4. График зависимости проекции скорости первого тела на ось Ox от времени изображается прямой, проходящей через точки (0; 6) и (3; 0), второго - через точки (0; 0) и (8; 4), где скорость задана в метрах в секунду, время - в секундах. Во сколько раз отличаются модули ускорений первого и второго тел?

Решение. Графики зависимости проекций скорости от времени для обоих тел показаны на рисунке.

Проекция ускорения первого тела определяется как тангенс тупого угла α 1 ; ее модуль вычисляем по формуле

| a x 1 | = | tg α 1 | = | tg (180 − α 3) | = 6 3 = 2 м/с 2 .

Первое тело движется равнозамедленно; величина его ускорения составляет a 1 = = 2 м/с 2 .

Проекция ускорения второго тела определяется как тангенс острого угла α 2 ; ее модуль вычисляем по формуле

a x 2 = tg α 2 = 4 8 = 0,5 м/с 2 .

Второе тело движется равноускоренно; величина его ускорения составляет a 2 = 0,5 м/с 2 .

Искомое отношение модулей ускорений первого и второго тел равно:

a 1 a 2 = 2 0,5 = 4 .

Величина ускорения первого тела больше величины ускорения второго тела в 4 раза.

Пример 5. График зависимости y -координаты от времени для первого тела изображается прямой, проходящей через точки (0; 0) и (5; 3), второго - через точки (3; 0) и (6; 6), где координата задана в метрах, время - в секундах. Определить отношение модулей проекций скоростей указанных тел.

Решение. Графики зависимости y -координаты от времени для обоих тел показаны на рисунке.

Проекция скорости первого тела определяется как тангенс угла α 1 ; ее модуль вычисляем по формуле

v y 1 = tg α 1 = 3 5 = 0,6 м/с.

Проекция скорости второго тела определяется как тангенс угла α 2 ; ее модуль вычисляем по формуле

v y 2 = tg α 2 = 6 3 = 2 м/с.

Обе проекции скоростей имеют положительный знак; следовательно, оба тела движутся равноускоренно.

Отношение модулей проекций скоростей указанных тел составляет:

| v y 2 | | v y 1 | = 2 0,6 ≈ 3 .

Величина проекции скорости второго тела больше величины проекции скорости второго тела приблизительно в 3 раза.

Пример 6. График зависимости скорости тела от времени изображается прямой, проходящей через точки (0; 4,0) и (2,5; 0), где скорость задана в метрах в секунду, время - в секундах. Во сколько раз путь, пройденный телом, больше модуля перемещения за 6,0 с движения?

Решение. График зависимости скорости тела от времени показан на рисунке. Точка остановки τ ост = 2,5 с попадает в интервал от 0 с до 6,0 с.

Следовательно, пройденный путь представляет собой сумму

S = S 1 + S 2 ,

а модуль перемещения - разность

| Δ r → | = | S 1 − S 2 | ,

где S 1 - путь, пройденный телом за интервал времени от 0 с до 2,5 с; S 2 - путь, пройденный телом за интервал времени от 2,5 с до 6,0 с.

Значения S 1 и S 2 рассчитаем графически как площади треугольников, показанных на рисунке:

S 1 = 1 2 ⋅ 4,0 ⋅ 2,5 = 5,0 м;

S 2 = 1 2 ⋅ (6,0 − 2,5) ⋅ 5,6 = 9,8 м.

Замечание : значение скорости v = 5,6 м/с в момент времени t = 6,0 c получено из подобия треугольников, т.е. из отношения

v 4,0 = 6,0 − 2,5 2,5 − 0 .

Вычислим пройденный путь:

S = S 1 + S 2 = 5,0 + 9,8 = 14,8 м

и величину перемещения:

| Δ r → | = | S 1 − S 2 | = | 5,0 − 9,8 | = 4,8 м.

Найдем искомое отношение пройденного пути и модуля перемещения:

S | Δ r → | = 14,8 4,8 ≈ 3,1 .

Пройденный путь приблизительно в 3,1 раза превышает величину перемещения.

3.1. Равнопеременное движение по прямой.

3.1.1. Равнопеременное движение по прямой - движение по прямой с постоянным по модулю и направлению ускорением:

3.1.2. Ускорение () - физическая векторная величина, показывающая, на сколько изменится скорость за 1 с.

В векторном виде:

где - начальная скорость тела, - скорость тела в момент времени t .

В проекции на ось Ox :

где - проекция начальной скорости на ось Ox , - проекция скорости тела на ось Ox в момент времени t .

Знаки проекций зависят от направления векторов и оси Ox .

3.1.3. График проекции ускорения от времени.

При равнопеременном движении ускорение постоянно, поэтому будет представлять собой прямые линии, параллельные оси времени (см. рис.):

3.1.4. Скорость при равнопеременном движении.

В векторном виде:

В проекции на ось Ox :

Для равноускоренного движения:

Для равнозамедленного движения:

3.1.5. График проекции скорости в зависимости от времени.

График проекции скорости от времени - прямая линия.

Направление движения: если график (или часть его) находятся над осью времени, то тело движется в положительном направлении оси Ox .

Значение ускорения: чем больше тангенс угла наклона (чем круче поднимается вверх или опускает вниз), тем больше модуль ускорения; где - изменение скорости за время

Пересечение с осью времени: если график пересекает ось времени, то до точки пересечения тело тормозило (равнозамедленное движение), а после точки пересечения начало разгоняться в противоположную сторону (равноускоренное движение).

3.1.6. Геометрический смысл площади под графиком в осях

Площадь под графиком, когда на оси Oy отложена скорость, а на оси Ox - время - это путь, пройденный телом.

На рис. 3.5 нарисован случай равноускоренного движения. Путь в данном случае будет равен площади трапеции: (3.9)

3.1.7. Формулы для расчета пути

Равноускоренное движение	Равнозамедленное движение
(3.10)	(3.12)
(3.11)	(3.13)
(3.14)

Все формулы, представленные в таблице, работают только при сохранении направления движения, то есть до пересечения прямой с осью времени на графике зависимости проекции скорости от времени.

Если же пересечение произошло, то движение проще разбить на два этапа:

до пересечения (торможение):

После пересечения (разгон, движение в обратную сторону)

В формулах выше - время от начала движения до пересечения с осью времени (время до остановки), - путь, который прошло тело от начала движения до пересечения с осью времени, - время, прошедшее с момента пересечения оси времени до данного момента t , - путь, который прошло тело в обратном направлении за время, прошедшее с момента пересечения оси времени до данного момента t , - модуль вектора перемещения за все время движения, L - путь, пройденный телом за все время движения.

3.1.8. Перемещение за -ую секунду.

За время тело пройдет путь:

За время тело пройдет путь:

Тогда за -ый промежуток тело пройдет путь:

За промежуток можно принимать любой отрезок времени. Чаще всего с.

Тогда за 1-ую секунду тело проходит путь:

За 2-ую секунду:

За 3-ю секунду:

Если внимательно посмотрим, то увидим, что и т. д.

Таким образом, приходим к формуле:

Словами: пути, проходимые телом за последовательные промежутки времени соотносятся между собой как ряд нечетных чисел, и это не зависит от того, с каким ускорением движется тело. Подчеркнем, что это соотношение справедливо при

3.1.9. Уравнение координаты тела при равнопеременном движении

Уравнение координаты

Знаки проекций начальной скорости и ускорения зависят от взаимного расположения соответствующих векторов и оси Ox .

Для решения задач к уравнению необходимо добавлять уравнение изменения проекции скорости на ось:

3.2. Графики кинематических величин при прямолинейном движении

3.3. Свободное падение тела

Под свободным падением подразумевается следующая физическая модель:

1) Падение происходит под действием силы тяжести:

2) Сопротивление воздуха отсутствует (в задачах иногда пишут «сопротивлением воздуха пренебречь»);

3) Все тела, независимо от массы падают с одинаковым ускорением (иногда добавляют - «независимо от формы тела», но мы рассматриваем движение только материальной точки, поэтому форма тела уже не учитывается);

4) Ускорение свободного падения направлено строго вниз и на поверхности Земли равно (в задачах часто принимаем для удобства подсчетов);

3.3.1. Уравнения движения в проекции на ось Oy

В отличии от движения по горизонтальной прямой, когда далеко не всех задач происходит смена направления движения, при свободном падении лучше всего сразу пользоваться уравнениями, записанными в проекциях на ось Oy .

Уравнение координаты тела:

Уравнение проекции скорости:

Как правило, в задачах удобно выбрать ось Oy следующим образом:

Ось Oy направлена вертикально вверх;

Начало координат совпадает с уровнем Земли или самой нижней точкой траектории.

При таком выборе уравнения и перепишутся в следующем виде:

3.4. Движение в плоскости Oxy .

Мы рассмотрели движение тела с ускорением вдоль прямой. Однако этим равнопеременное движение не ограничивается. Например, тело, брошенное под углом к горизонту. В таких задачах необходимо учитывать движение сразу по двум осям:

Или в векторном виде:

И изменение проекции скорости на обе оси:

3.5. Применение понятия производной и интеграла

Мы не будем приводить здесь подробное определение производной и интеграла. Для решения задач нам понадобятся лишь небольшой набор формул.

Производная:

где A , B и то есть постоянные величины.

Интеграл:

Теперь посмотрим, как понятие производной и интеграла применимо к физическим величинам. В математике производная обозначается «"», в физике производная по времени обозначается «∙» над функцией.

Скорость:

то есть скорость является производной от радиус-вектора.

Для проекции скорости:

Ускорение:

то есть ускорение является производной от скорости.

Для проекции ускорения:

Таким образом, если известен закон движения то легко можем найти и скорость и ускорение тела.

Теперь воспользуемся понятием интеграла.

Скорость:

то есть, скорость можно найти как интеграл по времени от ускорения.

Радиус-вектор:

то есть, радиус-вектор можно найти, взяв интеграл от функции скорости.

Таким образом, если известна функция то легко можем найти и скорость, и закон движения тела.

Константы в формулах определяются из начальных условий - значения и в момент времени

3.6. Треугольник скоростей и треугольник перемещений

3.6.1. Треугольник скоростей

В векторном виде при постоянном ускорении закон изменения скорости имеет вид (3.5):

Эта формула означает, что вектор равен векторной сумме векторов и Векторную сумму всегда можно изобразить на рисунке (см. рис.).

В каждой задаче, в зависимости от условий, треугольник скоростей будет иметь свой вид. Такое представление позволяет использовать при решении геометрические соображения, что часто упрощает решение задачи.

3.6.2. Треугольник перемещений

В векторном виде закон движения при постоянном ускорении имеет вид:

При решении задачи можно выбирать систему отсчета наиболее удобным образом, поэтому не теряя общности, можем выбрать систему отсчета так, что то есть начало системы координат помещаем в точку, где в начальный момент находится тело. Тогда

то есть вектор равен векторной сумме векторов и Изобразим на рисунке (см. рис.).

Как и в предыдущем случае в зависимости от условий треугольник перемещений будет иметь свой вид. Такое представление позволяет использовать при решении геометрические соображения, что часто упрощает решение задачи.

Определение

Равномерное прямолинейное движение -- это движение с постоянной скоростью, при котором ускорение отсутствует, а траектория движения представляет собой прямую линию.

Скорость равномерного прямолинейного движения не зависит от времени и в каждой точке траектории направлена так же, как и перемещение тела. То есть вектор перемещения совпадает по направлению с вектором скорости. При этом средняя скорость за любой промежуток времени равна мгновенной скорости: $\left\langle v\right\rangle =v$

Определение

Скорость равномерного прямолинейного движения -- это физическая векторная величина, равная отношению перемещения тела $\overrightarrow{S}$ за любой промежуток времени к значению этого промежутка t:

$$\overrightarrow{v}=\frac{\overrightarrow{S}}{t}$$

Таким образом, скорость равномерного прямолинейного движения показывает, какое перемещение совершает материальная точка за единицу времени.

Перемещение при равномерном прямолинейном движении определяется формулой:

$$ \overrightarrow{S} = \overrightarrow{v} \cdot t $$

Пройденный путь при прямолинейном движении равен модулю перемещения. Если положительное направление оси ОХ совпадает с направлением движения, то проекция скорости на ось ОХ равна величине скорости и положительна: $v_x = v$, то есть $v $>$ 0$

Проекция перемещения на ось ОХ равна: $s = v_t = x - x0$

где $x_0$ - начальная координата тела, $х$ - конечная координата тела (или координата тела в любой момент времени)

Уравнение движения, то есть зависимость координаты тела от времени $х = х(t)$, принимает вид: $х = x_0 + v_t$

Если положительное направление оси ОХ противоположно направлению движения тела, то проекция скорости тела на ось ОХ отрицательна, скорость меньше нуля ($v $

Зависимость проекции скорости тела от времени показана на рис. 1. Так как скорость постоянна ($v = const$), то графиком скорости является прямая линия, параллельная оси времени Ot.

Рис. 1. Зависимость проекции скорости тела от времени при равномерном прямолинейном движении.

Проекция перемещения на координатную ось численно равна площади прямоугольника ОАВС (рис. 2), так как величина вектора перемещения равна произведению вектора скорости на время, за которое было совершено перемещение.

Рис. 2. Зависимость проекции перемещения тела от времени при равномерном прямолинейном движении.

График зависимости перемещения от времени показан на рис. 3. Из графика видно, что проекция скорости на ось Ot численно равна тангенсу угла наклона графика к оси времени:

Рис. 3. Зависимость проекции перемещения тела от времени при равномерном прямолинейном движении.

Зависимость координаты от времени показана на рис. 4. Из рисунка видно, что

tg $\alpha $1 $>$ tg $\alpha $2, следовательно, скорость тела 1 выше скорости тела 2 (v1 $>$ v2).

tg $\alpha $3 = v3 $

Рис. 4. Зависимость координаты тела от времени при равномерном прямолинейном движении.

Если тело покоится, то графиком координаты является прямая, параллельная оси времени, то есть х = х0

Задача 1

Два поезда движутся на встречу друг другу по параллельным рельсам. Скорость первого поезда 10 метров в секунду, длина первого поезда 500 метров. Скорость второго поезда 30 метров в секунду, длина второго поезда 300 метров. Определить в течение какого времени второй поезд будет ехать мимо первого.

Дано: $v_1$=10 м/с; $v_2$=30 м/с; $L_1$=500 м; $L_2$=300 м

Найти: t --- ?

Время, в течение которого поезда будут проходить мимо друг друга, можно определить, разделив общую длину поездов на их относительную скорость. Скорость первого поезда относительно второго определяется по формуле v= v1+v2 Тогда формула для определения времени принимает вид: $t=\frac{L_1+L_2}{v_1+v_2}=\frac{500+300}{10+30}=20\ c$

Ответ: второй поезд будет ехать мимо первого в течение 20 секунд.

Задача 2

Определить скорость течения реки и скорость катера в стоячей воде, если известно, что катер проходит расстояние 300 километров по течению за 4 часа, а против течения -- за 6 часов.

Дано: $L$=300000 м; $t_1$=14400 с; $t_2$=21600 с

Найти: $v_p$ - ?; $v_k$ - ?

Скорость катера по течению реки относительно берега $v_1=v_k+v_p$, а против течения $v_2=v_k-v_p$ . Запишем закон движения для обоих случаев:

Решив уравнения относительно vp и vk, получаем формулы для расчета скорости течения реки и скорости катера.

Скорость течения реки: $v_p=\frac{L\left(t_2-t_1\right)}{2t_1t_2}=\frac{300000\left(21600-14400\right)}{2\times 14400\times 21600}=3,47\ м/с$

Скорость катера: $v_к=\frac{L\left(t_2+t_1\right)}{2t_1t_2}=\frac{300000\left(21600+14400\right)}{2\times 14400\times 21600}=17,36\ м/с$

Ответ: скорость течения реки равна 3,47 метров в секунду, скорость катера равна 17,36 метров в секунду.

Скорость является одной из основных характеристик . Она выражает саму суть движения, т.е. определяет то отличие, которое имеется между телом неподвижным и телом движущимся.

Единицей измерения скорости в системе СИ является м/с .

Важно помнить, что скорость – величина векторная. Направление вектора скорости определяется по движения. Вектор скорости всегда направлен по касательной к траектории в той точке, через которую проходит движущееся тело (рис.1).

К примеру, рассмотрим колесо движущегося автомобиля. Колесо вращается и все точки колеса движутся по окружностям. Брызги, разлетающиеся от колеса, будут лететь по касательным к этим окружностям, указывая направления векторов скоростей отдельных точек колеса.

Таким образом, скорость характеризует направление движения тела (направление вектора скорости) и быстроту его перемещения (модуль вектора скорости).

Отрицательная скорость

Может ли скорость тела быть отрицательной? Да, может. Если скорость тела отрицательна, это значит, что тело движется в направлении, противоположном направлению оси координат в выбранной системе отсчета. На рис.2 изображено движение автобуса и автомобиля. Скорость автомобиля отрицательна, а скорость автобуса положительна. Следует помнить, что говоря о знаке скорости, мы имеем ввиду проекцию вектора скорости на координатную ось.

Равномерное и неравномерно движение

В общем случае скорость зависит от времени. По характеру зависимости скорости от времени, движение бывает равномерное и неравномерно.

ОПРЕДЕЛЕНИЕ

Равномерное движение – это движение с постоянной по модулю скоростью.

В случае неравномерного движения говорят о :

Примеры решения задач по теме «Скорость»

ПРИМЕР 1

Задание	Автомобиль прошел первую половину пути между двумя населенными пунктами со скоростью 90 км/ч, а вторую половину – со скоростью 54 км/ч. Определите среднюю скорость автомобиля.
Решение	Было бы неверным вычислять среднюю скорость автомобиля как среднее арифметическое двух указанных скоростей. Воспользуемся определением средней скорости: Так как предполагается прямолинейное равномерное движение, знаки векторов можно опустить. Время, потраченное автомобилем на прохождение всего отрезка пути: где — время, затраченное на прохождение первой половины пути, а — время, затраченное на прохождение второй половины пути. Суммарное перемещение равно расстоянию между населенными пунктами, т.е. . Подставив эти соотношения в формулу для средней скорости, получим: Переведем скорости на отдельных участках в систему СИ: Тогда средняя скорость автомобиля: (м/с)
Ответ	Средняя скорость автомобиля равна 18,8 м/с

ПРИМЕР 2

Задание	Автомобиль проехал 10 секунд со скоростью 10 м/с, а затем ехал еще 2 минуты со скоростью 25 м/с. Определить среднюю скорость автомобиля.
Решение	Сделаем рисунок.