Позволяет нам существовать на этой планете. Как можно понять, что представляет собой центростремительное ускорение? Определение этой физической величины представлено ниже.

Наблюдения

Самый простой пример ускорения тела, движущегося по окружности, можно наблюдать, вращая камень на веревке. Вы тянете веревку, а веревка тянет камень к центру. В каждый момент времени веревка сообщает камню некоторое количество движения, и каждый раз - в новом направлении. Можно представить движение веревки в виде серии слабых рывков. Рывок - и веревка изменяет свое направление, еще рывок - еще раз изменение, и так по кругу. Если вы внезапно отпустите веревку, рывки прекратятся, а вместе с ними и прекратится изменение направления скорости. Камень будет двигаться в направлении касательной к кругу. Возникает вопрос: "С каким ускорением будет двигаться тело в это мгновение?"

Формула центростремительного ускорения

Прежде всего стоит заметить, что движение тела по окружности является сложным. Камень участвует в двух видах движения одновременно: под действием силы он движется к центру вращения, и одновременно по касательной к окружности, от этого центра удаляется. Согласно Второму закону Ньютона, сила, удерживающая камень на веревке, направлена к центру вращения вдоль этой веревки. Туда же будет направлен вектор ускорения.

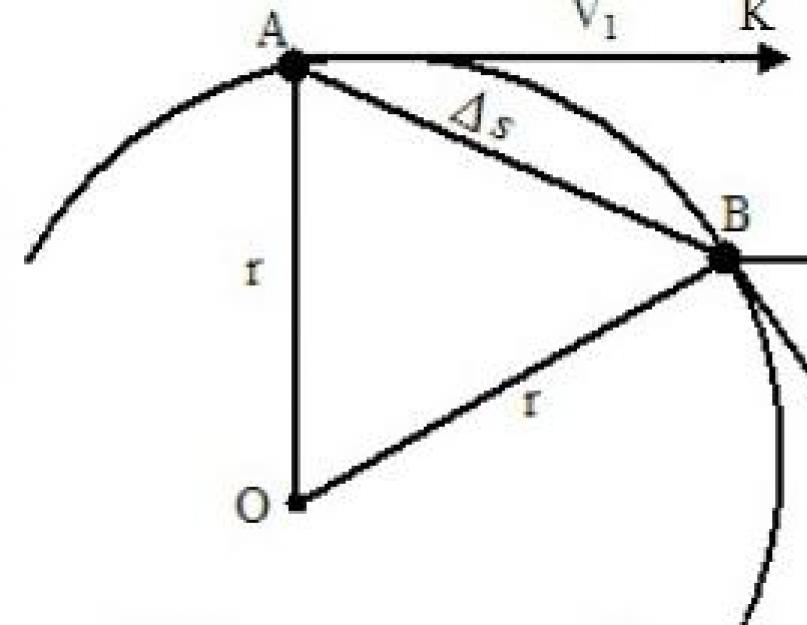
Пусть за некоторое время t наш камень, равномерно двигаясь со скоростью V, попадает из точки A в точку B. Предположим, что в момент времени, когда тело пересекало точку B, на него перестала действовать центростремительная сила. Тогда за промежуток времени оно попало бы в точку K. Она лежит на касательной. Если бы в тот же момент времени на тело действовали бы только центростремительные силы, то за время t, двигаясь с одинаковым ускорением, оно оказалось бы в точке O, которая расположена на прямой, представляющей собой диаметр окружности. Оба отрезка являются векторами и подчиняются правилу векторного сложения. В результате суммирования этих двух движений за отрезок времени t получаем результирующую движения по дуге AB.

Если промежуток времени t взять пренебрежимо малым, то дуга AB будет мало отличаться от хорды AB. Таким образом, можно заменить движение по дуге движением по хорде. В этом случае перемещение камня по хорде будет подчиняться законам прямолинейного движения, то есть пройденное расстояние AB будет равно произведению скорости камня на время его движения. AB = V х t.

Обозначим искомое центростремительное ускорение буквой a. Тогда пройденный только под действием центростремительного ускорения путь можно рассчитать по формуле равноускоренного движения:

Расстояние AB равно произведению скорости и времени, то есть AB = V х t,

AO - вычислено ранее по формуле равноускоренного движения для перемещения по прямой: AO = at 2 / 2.

Подставляя эти данные в формулу и преобразуя их, получаем простую и изящную формулу центростремительного ускорения:

Словами это можно выразить так: центростремительное ускорение тела, двигающегося по окружности, равно частному от деления линейной скорости в квадрате на радиус окружности, по которой вращается тело. Центростремительная сила в таком случае будет выглядеть так, как на картинке ниже.

Угловая скорость

Угловая скорость равна частному от деления линейной скорости на радиус окружности. Верно и обратное утверждение: V = ωR, где ω - угловая скорость

Если подставить это значение в формулу, можно получить выражение центробежного ускорения для угловой скорости. Оно будет выглядеть так:

Ускорение без изменения скорости

И все же, отчего тело с ускорением, направленным к центру, не движется быстрее и не перемещается ближе к центру вращения? Ответ кроется в самой формулировке ускорения. Факты говорят о том, что движение по окружности реально, но для его поддержания требуется ускорение, направленное к центру. Под действием силы, вызванной данным ускорением, происходит изменение количества движения, в результате чего траектория движения постоянно искривляется, все время меняя направление вектора скорости, но не изменяя ее абсолютной величины. Двигаясь по кругу, наш многострадальный камень устремляется внутрь, в противном случае он продолжал бы двигаться по касательной. Каждое мгновение времени, уходя по касательной, камень притягивается к центру, но не попадает в него. Еще одним примером центростремительного ускорения может стать водный лыжник, описывающий небольшие круги на воде. Фигура спортсмена наклонена; он как бы падает, продолжая движение и наклонившись вперед.

Таким образом, можно сделать вывод о том, что ускорение не увеличивает скорость тела, так как векторы скорости и ускорения перпендикулярны друг к другу. Добавляясь к вектору скорости, ускорение лишь меняет направление движения и удерживает тело на орбите.

Превышение запаса прочности

В предыдущем опыте мы имели дело с идеальной веревкой, которая не рвалась. Но, допустим, наша веревка самая обычная, и даже можно вычислить усилие, после которого она просто порвется. Для того чтобы рассчитать эту силу, достаточно сопоставить запас прочности веревки с нагрузкой, которую она испытывает в процессе вращения камня. Вращая камень с большей скоростью, вы сообщаете ему большее количество движения, а значит, и большее ускорение.

При диаметре джутовой веревки около 20 мм ее прочность на разрыв равна около 26 кН. Примечательно, что длина веревки нигде не фигурирует. Вращая груз размером в 1 кг на веревке радиусом в 1 м, можно вычислить, что линейная скорость, необходимая для ее разрыва равна 26 х 10 3 = 1кг х V 2 / 1 м. Таким образом, скорость, которую опасно превышать, будет равна √26 х 10 3 = 161 м/с.

Сила тяжести

При рассмотрении опыта мы пренебрегали действием силы тяжести, так как при таких больших скоростях ее влияние пренебрежимо мало. Но можно заметить, что при раскручивании длинной веревки тело описывает более сложную траекторию и постепенно приближается к земле.

Небесные тела

Если перенести законы движения по окружности в космос и применить их к движению небесных тел, можно заново открыть несколько давно знакомых формул. Например, сила, с которой тело притягивается к Земле, известна по формуле:

В нашем случае множитель g и является тем самым центростремительным ускорением, которое было выведено из предыдущей формулы. Только в этом случае роль камня будет выполнять небесное тело, притягивающееся к Земле, а роль веревки - сила земного притяжения. Множитель g будет выражен через радиус нашей планеты и скорость ее вращения.

Итоги

Сущность центростремительного ускорения состоит в тяжелой и неблагодарной работе удержания движущегося тела на орбите. Наблюдается парадоксальный случай, когда при постоянном ускорении тело не изменяет величины своей скорости. Для неподготовленного ума такое заявление довольно парадоксально. Тем не менее и при расчете движения электрона вокруг ядра, и при вычислении скорости вращения звезды вокруг черной дыры, центростремительной ускорение играет не самую последнюю роль.

При равномерном движении по окружности тело движется с центростремительным ускорением. Определим это ускорение.

Ускорение направлено туда же, куда и изменение скорости, следовательно, ускорение направлено к центру окружности. Важное допущение: угол настолько мал, что длина хордыABсовпадает с длиной дуги:

по двум пропорциональным сторонам и углу между ними. Следовательно:

–модуль центростремительного ускорения.

Основы динамики Первый закон Ньютона. Инерциальные системы отсчета. Принцип относительности Галилея

Любое тело остается неподвижным, пока на него не действуют другие тела. Тело, двигавшееся с некоторой скоростью, продолжает двигаться равномерно и прямолинейно до тех пор, пока не него не подействуют другие тела. К таким выводам о законах движения тел впервые пришел итальянский ученый Галилео Галилей.

Явление сохранения скорости движения тела при отсутствии внешних воздействий называется инерцией .

Всякий покой и движение тел относительны. Одно и то же тело может находиться в состоянии покоя в одной системе отсчета и двигаться с ускорением в другой. Но существуют такие системы отсчета, относительно которых поступательно движущиеся тела сохраняют свою скорость постоянной, если на них не действуют другие тела . Это утверждение называется первым законом Ньютона (законом инерции).

Системы отсчета, относительно которых тело при отсутствии внешних воздействий движется прямолинейно и равномерно, называют инерциальными системами отсчета .

Инерциальных систем отсчета может быть сколь угодно много, т.е. любая система отсчета, которая движется равномерно и прямолинейно по отношению к инерциальной, также является инерциальной. Истинных (абсолютных) инерциальных систем отсчета нет.

Причиной изменения скорости движения тел всегда является его взаимодействие с другими телами.

При взаимодействии двух тел всегда изменяются скорости и первого, и второго тела, т.е. оба тела приобретают ускорения. Ускорения двух взаимодействующих тел могут быть различными, они зависят от инертности тел.

Инертность – способность тела сохранять свое состояние движения (покоя). Чем больше инертность тела, тем меньшее ускорение оно приобретет при взаимодействии с другими телами, и тем будет ближе его движение к равномерному прямолинейному движению по инерции.

Масса – физическая величина, характеризующая инертность тела. Чем большей массой обладает тело, тем меньшее ускорение оно получает при взаимодействии.

За единицу массы в СИ принят килограмм: [m]=1 кг.

В инерциальных системах отсчета любое изменение скорости тела происходит под действием других тел. Сила – это количественное выражение действия одного тела на другое.

Сила – векторная физическая величина, за ее направление принимают направление ускорения тела, которое вызывается этой силой. У силы всегда есть точка приложения.

В СИ за единицу силы принимаются сила, которая телу массой 1 кг сообщает ускорение 1 м/с 2 . Эта единица называется Ньютоном:

.

Второй закон Ньютона

Сила, действующая на тело, равна произведению массы тела на сообщаемое этой силой ускорение :

.

Таким образом, ускорение тела прямо пропорционально действующей на тело силе и обратно пропорционально его массе:

.

Равномерное движение по окружности характеризуется движением тела вдоль окружности. При этом меняется только направление скорости, а ее модуль остаётся постоянным.

В общем случае тело движется по криволинейной траектории, и его сложно описать. Для упрощения описания криволинейного движения его разбивают на более простые виды движения. В частности один из таких видов и является равномерное движение по окружности. Любую кривую траекторию движения можно разбить на участки достаточно малой величины, на которых тело будет приближённо двигаться по дуге являющуюся частью окружности.

При движении тела по окружности линейная скорость направлена по касательной. Следовательно, даже если тело движется по дуге с постоянной по модулю скоростью, то направление движения в каждой точке будет разным. Таки образом всякое движение по окружности является движением с ускорением.

Представьте себе окружность, по которой движется материальная точка. В нулевой момент времени она находится в положении A. Через некоторый интервал времени она оказывается в точке B. Если провести два радиус вектор из центра окружности к точке A и точке B, то между ними получится некоторый угол. Назовем его угол фи. Если за одинаковые промежутки времени точка поворачивается на одинаковый угол фи, то такое движение называется равномерным, а скорость называется угловой.

Рисунок 1 - угловая скорость.

Угловая скорость измеряется в оборотах в секунду. Один оборот в секунду это когда точка проходит вдоль всей окружности и возвращается в начальное положение, затратив на это одну секунду. Такой оборот называется периодом обращения. Величина обратная периоду вращения называется частота вращения. То есть сколько оборотов успевает совершить точка в течении одной секунды. Угол образованный двумя радиус векторами измеряется в радианах. Радиан это угол между двумя радиус векторами, которые вырезают на поверхности окружности дугу длинной в радиус.

Скорость движения точки по окружности можно измерять и в радианах в с секунду. В таком случае перемещение точки на один радиан в секунду и называется скоростью. Такая скорость называется угловой. То есть на какое количество единичных углов успевает повернуться радиус вектор в течении одной секунды. При равномерном движении по окружности угловая скорость постоянна.

Для определения ускорения движения по окружности построим на рисунке вектора скорости точек А и В. Угол между этими векторами равен углу между радиус векторами. Так как ускорение это разница между скоростями, взятыми через определенный интервал времени деленная на этот интервал. То с помощью параллельного переноса перенесем начало вектора скорости в точке А в точку В. Разностью этих векторов будет вектор дельта V. Если его разделить на хорду соединяющую точки А и В, при условии что расстояние между точками бесконечно мало, то мы и получим вектор ускорения направленный к центру окружности. Который так же называют центростремительным ускорением.

Так как линейная скорость равномерно меняет направление, то движение по окружности нельзя назватьравномерным , оно являетсяравноускоренным .

Угловая скорость

Выберем на окружности точку1 . Построим радиус. За единицу времени точка переместится в пункт2 . При этом радиус описывает угол. Угловая скорость численно равна углу поворота радиуса за единицу времени.

Период и частота

Период вращенияT - это время, за которое тело совершает один оборот.

Частота вращение - это количество оборотов за одну секунду.

Частота и период взаимосвязаны соотношением

Связь с угловой скоростью

Линейная скорость

Каждая точка на окружности движется с некоторой скоростью. Эту скорость называют линейной.Направление вектора линейной скорости всегда совпадает с касательной к окружности. Например, искры из-под точильного станка двигаются, повторяя направление мгновенной скорости.

Рассмотрим точку на окружности, которая совершает один оборот, время, которое затрачено - это есть периодT .Путь , который преодолевает точка - это есть длина окружности.

Центростремительное ускорение

При движении по окружности вектор ускорения всегда перпендикулярен вектору скорости, направлен в центр окружности.

Используя предыдущие формулы, можно вывести следующие соотношения

Точки, лежащие на одной прямой исходящей из центра окружности (например, это могут быть точки, которые лежат на спице колеса), будут иметь одинаковые угловые скорости, период и частоту. То есть они будут вращаться одинаково, но с разными линейными скоростями. Чем дальше точка от центра, тем быстрей она будет двигаться.

Закон сложения скоростей справедлив и для вращательного движения. Если движение тела или системы отсчета не является равномерным, то закон применяется для мгновенных скоростей. Например, скорость человека, идущего по краю вращающейся карусели, равна векторной сумме линейной скорости вращения края карусели и скорости движения человека.

Земля участвует в двух основных вращательных движениях: суточном (вокруг своей оси) и орбитальном (вокруг Солнца). Период вращения Земли вокруг Солнца составляет 1 год или 365 суток. Вокруг своей оси Земля вращается с запада на восток, период этого вращения составляет 1 сутки или 24 часа. Широтой называется угол между плоскостью экватора и направлением из центра Земли на точку ее поверхности.

Согласно второму закону Ньютона причиной любого ускорения является сила. Если движущееся тело испытывает центростремительное ускорение, то природа сил, действием которых вызвано это ускорение, может быть различной. Например, если тело движется по окружности на привязанной к нему веревке, то действующей силой является сила упругости.

Если тело, лежащее на диске, вращается вместе с диском вокруг его оси, то такой силой является сила трения. Если сила прекратит свое действие, то далее тело будет двигаться по прямой

Рассмотрим перемещение точки на окружности из А в В. Линейная скорость равна

Теперь перейдем в неподвижную систему, связанную с землей. Полное ускорение точки А останется прежним и по модулю, и по направлению, так как при переходе от одной инерциальной системы отсчета к другой ускорение не меняется. С точки зрения неподвижного наблюдателя траектория точки А - уже не окружность, а более сложная кривая (циклоида), вдоль которой точка движется неравномерно.

Центростремительное ускорение - компонента ускорения точки, характеризующая быстроту изменения направления вектора скорости для траектории с кривизной (вторая компонента, тангенциальное ускорение , характеризует изменение модуля скорости). Направлено к центру кривизны траектории, чем и обусловлен термин. По величине равно квадрату скорости, поделённому на радиус кривизны. Термин «центростремительное ускорение» эквивалентен термину «нормальное ускорение ». Ту составляющую суммы сил, которая обуславливает это ускорение, называют центростремительной силой .

Наиболее простым примером центростремительного ускорения является вектор ускорения при равномерном движении по окружности (направленный к центру окружности).

Осестремительное ускорение в проекции на плоскость, перпендикулярную оси, предстаёт как центростремительное.

Энциклопедичный YouTube

• 1 / 5

  A n = v 2 R {\displaystyle a_{n}={\frac {v^{2}}{R}}\ } a n = ω 2 R , {\displaystyle a_{n}=\omega ^{2}R\ ,}

  где a n {\displaystyle a_{n}\ } - нормальное (центростремительное) ускорение, v {\displaystyle v\ } - (мгновенная) линейная скорость движения по траектории, ω {\displaystyle \omega \ } - (мгновенная) угловая скорость этого движения относительно центра кривизны траектории, R {\displaystyle R\ } - радиус кривизны траектории в данной точке. (Связь между первой формулой и второй очевидна, учитывая v = ω R {\displaystyle v=\omega R\ } ).

  Выражения выше включают абсолютные величины. Их легко записать в векторном виде, домножив на e R {\displaystyle \mathbf {e} _{R}} - единичный вектор от центра кривизны траектории к данной её точке:

  a n = v 2 R e R = v 2 R 2 R {\displaystyle \mathbf {a} _{n}={\frac {v^{2}}{R}}\mathbf {e} _{R}={\frac {v^{2}}{R^{2}}}\mathbf {R} } a n = ω 2 R . {\displaystyle \mathbf {a} _{n}=\omega ^{2}\mathbf {R} .}

  Эти формулы равно применимы к случаю движения с постоянной (по абсолютной величине) скоростью, так и к произвольному случаю. Однако во втором надо иметь в виду, что центростремительное ускорение не есть полный вектор ускорения, а лишь его составляющая, перпендикулярная траектории (или, что то же, перпендикулярная вектору мгновенной скорости); в полный же вектор ускорения тогда входит еще и тангенциальная составляющая (тангенциальное ускорение ) a τ = d v / d t {\displaystyle a_{\tau }=dv/dt\ } , по направлению совпадающее с касательной к траектории (или, что то же, с мгновенной скоростью) .

  Мотивация и вывод

  То, что разложение вектора ускорения на компоненты - одну вдоль касательного к траектории вектора (тангенциальное ускорение) и другую ортогональную ему (нормальное ускорение) - может быть удобным и полезным, довольно очевидно само по себе. При движении с постоянной по модулю скоростью тангенциальная составляющая становится равной нулю, то есть в этом важном частном случае остается только нормальная составляющая. Кроме того, как можно увидеть ниже, каждая из этих составляющих имеет ярко выраженные собственные свойства и структуру, и нормальное ускорение содержит в структуре своей формулы достаточно важное и нетривиальное геометрическое наполнение. Не говоря уже о важном частном случае движения по окружности.

  Формальный вывод

  Разложение ускорения на тангенциальную и нормальную компоненты (вторая из которых и есть центростремительное или нормальное ускорение) можно найти, продифференцировав по времени вектор скорости , представленный в виде v = v e τ {\displaystyle \mathbf {v} =v\,\mathbf {e} _{\tau }} через единичный вектор касательной e τ {\displaystyle \mathbf {e} _{\tau }} :

  a = d v d t = d (v e τ) d t = d v d t e τ + v d e τ d t = d v d t e τ + v d e τ d l d l d t = d v d t e τ + v 2 R e n , {\displaystyle \mathbf {a} ={\frac {d\mathbf {v} }{dt}}={\frac {d(v\mathbf {e} _{\tau })}{dt}}={\frac {\mathrm {d} v}{\mathrm {d} t}}\mathbf {e} _{\tau }+v{\frac {d\mathbf {e} _{\tau }}{dt}}={\frac {\mathrm {d} v}{\mathrm {d} t}}\mathbf {e} _{\tau }+v{\frac {d\mathbf {e} _{\tau }}{dl}}{\frac {dl}{dt}}={\frac {\mathrm {d} v}{\mathrm {d} t}}\mathbf {e} _{\tau }+{\frac {v^{2}}{R}}\mathbf {e} _{n}\ ,}

  Здесь использовано обозначение для единичного вектора нормали к траектории и l {\displaystyle l\ } - для текущей длины траектории ( l = l (t) {\displaystyle l=l(t)\ } ); в последнем переходе также использовано очевидное

  d l / d t = v {\displaystyle dl/dt=v\ }

  и, из геометрических соображений,

  d e τ d l = e n R . {\displaystyle {\frac {d\mathbf {e} _{\tau }}{dl}}={\frac {\mathbf {e} _{n}}{R}}.} v 2 R e n {\displaystyle {\frac {v^{2}}{R}}\mathbf {e} _{n}\ }

  Нормальным (центростремительным) ускорением. При этом его смысл, смысл входящих в него объектов, а также доказательство того факта, что он действительно ортогонален касательному вектору (то есть что e n {\displaystyle \mathbf {e} _{n}\ } - действительно вектор нормали) - будет следовать из геометрических соображений (впрочем, то, что производная любого вектора постоянной длины по времени перпендикулярна самому этому вектору, - достаточно простой факт; в данном случае мы применяем это утверждение для d e τ d t {\displaystyle {\frac {d\mathbf {e} _{\tau }}{dt}}}

  Замечания

  Легко заметить, что абсолютная величина тангенциального ускорения зависит только от путевого ускорения, совпадая с его абсолютной величиной, в отличие от абсолютной величины нормального ускорения, которая от путевого ускорения не зависит, зато зависит от путевой скорости.

  Приведенные здесь способы или их варианты могут быть использованы для введения таких понятий, как кривизна кривой и радиус кривизны кривой (поскольку в случае, когда кривая - окружность, R {\displaystyle R} совпадает с радиусом такой окружности; не слишком трудно также показать, что окружность в плоскости e τ , e n {\displaystyle \mathbf {e} _{\tau },\,e_{n}} с центром в направлении e n {\displaystyle e_{n}\ } от данной точки на расстоянии R {\displaystyle R} от неё - будет совпадать с данной кривой - траекторией - с точностью до второго порядка малости по расстоянию до данной точки).

  История

  Первым правильные формулы для центростремительного ускорения (или центробежной силы) получил, по-видимому, Гюйгенс . Практически с этого времени рассмотрение центростремительного ускорения входит в обычную технику решения механических задач и т.д.

  Несколько позже эти формулы сыграли существенную роль в открытии закона всемирного тяготения (формула центростремительного ускорения использовалась для получения закона зависимости гравитационной силы от расстояния до источника гравитации, исходя из выведенного из наблюдений третьего закона Кеплера).

  К XIX веку рассмотрение центростремительного ускорения становится уже совершенно рутинным как для чистой науки, так и для инженерных приложений.