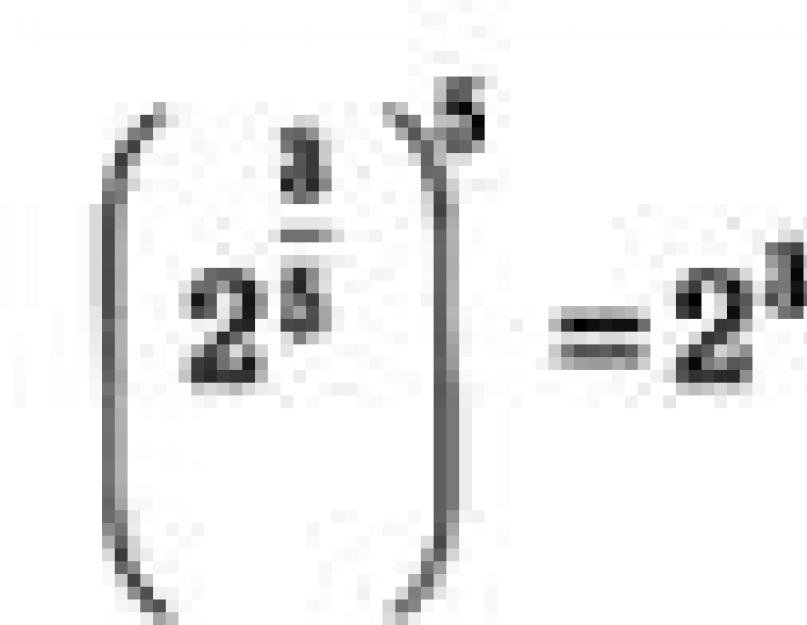Урок и презентация на тему: "Обобщение понятий о показателях степени"

Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания! Все материалы проверены антивирусной программой.

Обучающие пособия и тренажеры в интернет-магазине "Интеграл" для 11 класса
Алгебраические задачи с параметрами, 9–11 классы
Программная среда "1С: Математический конструктор 6.1"

Ребята, на этом уроке мы займемся обобщением знаний о показателях степеней. Мы умеем вычислять степени с любым целочисленным показателем. Как быть, если показатель степени - не целое число? И какая связь между корнями и степенными функциями не целого показателя?

Давайте немного повторим, рассмотрим число вида $a^n$.
1. Если $n=0$, то $a^n=a^0=1$.
2. Если $n=1$, то $a^n=a^1=a$.
3. Если $n=2,3,4,5$… то $a^n=a*a*a…*a$ (n множителей).
4. Если $n=1,2,3,4,5$… и $а≠0$, то $a^{-n}=\frac{1}{a^n}$.
Указанные выше правила можно также использовать как памятку!

Во всех представленных выше правилах, показатель степени - целое число. Как быть в случае дробного показателя степени?
Что представляет из себя число $2^{\frac{2}{3}}$ и как с ним работать? При работе с такими степенями нужно, чтобы все свойства для целочисленных степеней сохранялись. Например, при возведении степени в степень – показатели перемножались.

Например: ${(2^{\frac{2}{3}})}^3=2^{\frac{2}{3}*3}=2^2$.
Давайте введем вот такую замену символов: $a=2^{\frac{2}{3}}$.
Тогда: $a^3=2^2$.
Получаем: $a=\sqrt{2^2}$.
То есть мы можем представить исходное выражение в таком виде: $2^{\frac{2}{3}}=\sqrt{2^2}$.

Определение. Пусть нам дана обыкновенная дробь $\frac{a}{b}$, $b≠1$ и $х≥0$, тогда $x^{\frac{a}{b}}=\sqrt[b]{x^a}$.

Например: $3^{\frac{1}{3}}=\sqrt{3}$,
$5^{\frac{2}{5}}=\sqrt{5^2}$.

Давайте умножим два числа с одинаковыми основаниями, но разными степенями:
$a^{\frac{2}{3}}*a^{\frac{1}{4}}=\sqrt{a^2}*\sqrt{a}=\sqrt{a^8}*\sqrt{a^3}=\sqrt{a^{11}}=a^{\frac{11}{12}}$.
Но заметим так же: $\frac{2}{3}+\frac{1}{4}=\frac{8+3}{12}=\frac{11}{12}$.
То есть: $a^{\frac{2}{3}}*a^{\frac{1}{4}}=a^{\frac{2}{3}+\frac{1}{4}}=a^{\frac{11}{12}}$.
Складывать дроби гораздо проще, чем работать с радикалами (нужно привести показатели к одинаковому виду и потом только перемножать). Поэтому принято переходить к степенным функциям с дробным показателем.

Пример.
Вычислить:
а) ${(27)}^{\frac{1}{3}}$.
б) ${(32)}^{\frac{3}{5}}$.
в) $0^{\frac{5}{7}}$.
г) ${(-32)}^{\frac{1}{5}}$.
Решение.
а) ${(27)}^{\frac{1}{3}}=\sqrt{27}=3$.

Б) ${(32)}^{\frac{3}{5}}=\sqrt{{32}^3}={(\sqrt{32})}^3=2^3=8$.

В) $0^{\frac{5}{7}}=\sqrt{0^5}={(\sqrt{0})}^5=0^5=0$.

Г) Извлекать корень с дробным показателем мы можем только из положительного числа, ребята посмотрите на наше определение. Наше выражение не имеет смысла.
Кажется ${(-32)}^{\frac{1}{5}}=\sqrt{-32}=-2$ - верная запись, но давайте внимательно посмотрим на наше выражение: ${(-32)}^{\frac{1}{5}}$=${(-32)}^{\frac{2}{10}}$=$\sqrt{{(-32)}^2}$=$\sqrt{1024}=2$.
Получили противоречивое выражение, хотя все операции выполнены верно, согласно свойствам и определениям. Поэтому математики запретили возводить в дробную степень отрицательные числа.

Ребята, запомните: в дробную степень мы можем возводить только положительные числа!

Определение. Пусть дана обыкновенная дробь $\frac{a}{b}$, $b≠1$ и $х>0$, тогда $x^{-\frac{p}{q}}=\frac{1}{x^{\frac{p}{q}}}$.

Например: $2^{-\frac{1}{4}}=\frac{1}{2^{\frac{1}{4}}}=\frac{1}{\sqrt{2}}$.
$3^{-\frac{3}{5}}=\frac{1}{3^{\frac{3}{5}}}=\frac{1}{\sqrt{3^3}}=\frac{1}{\sqrt{27}}$.

Все свойства с которыми мы сталкивались при работе со степенными числами сохраняются и в случае рациональных степеней, давайте повторим свойства.

Пусть нам даны положительные числа $a>0$ и $b>0$, x и y – произвольные рациональные числа, тогда выполняются следующие 5 свойств:
1. $a^x*a^y=a^{x+y}$.
2. $\frac{a^x}{a^y}=a^{x-y}$.
3. ${(a^x}^y=a^{x*y}$.
4. $(a*b)^x=a^x*a^y$.
5. ${(\frac{a}{b})}^x=\frac{a^x}{b^x}$.

Пример.
Упростите выражение: $\frac{\sqrt{x}}{x^{\frac{1}{2}}+y^{\frac{1}{2}}}+\frac{\sqrt{y}}{x^{\frac{1}{2}}-y^{\frac{1}{2}}}$.
Решение.
Перепишем числители в виде степенных функций:
$\frac{x^{\frac{1}{2}}}{x^{\frac{1}{2}}+y^{\frac{1}{2}}}+\frac{y^{\frac{1}{2}}}{x^{\frac{1}{2}}-y^{\frac{1}{2}}}$.
Приведем к общему знаменателю:
$\frac{x^{\frac{1}{2}}(x^{\frac{1}{2}}-y^{\frac{1}{2}})+y^{\frac{1}{2}}(x^{\frac{1}{2}}+y^{\frac{1}{2}})}{(x^{\frac{1}{2}}+y^{\frac{1}{2}})(x^{\frac{1}{2}}-y^{\frac{1}{2})}}$ =$\frac{x-x^{\frac{1}{2}}*y^{\frac{1}{2}}+y^{\frac{1}{2}}*x^{\frac{1}{2}}+y}{x-y}$=$\frac{x+y}{x-y}$.

Пример.
Решить уравнения:
а) $\sqrt{x^4}=1$.
б) $x^{\frac{4}{5}}=1$.
Решение.
а) Возведем обе части уравнения в пятую степень:
$x^4=1$.
$x=±1$.

Б) Наше уравнение очень похоже на предыдущие. Если мы перейдем от записи корней к степенным функциям, то запись получится идентичная, но стоит учесть, что у нас сразу дано степенное выражение. По определению число х может быть только положительным, тогда у нас остается один ответ $х=1$.

Пример.
Решить уравнение: $x^{-\frac{2}{5}}+x^{-\frac{1}{5}}-12=0$.
Решение.
Давайте введем новую переменную: $y=x^{-\frac{1}{5}}$.
$y^2={(x^{-\frac{1}{5}})}^2=x^{-\frac{2}{5}}$.
Тогда наше уравнение примет вид обычного квадратного уравнения: $y^2+y-12=0$.
Решив уравнение, получим два корня: $y_1=-4$ и $y_2=3$.

Нам остается решить два уравнения: $x^{-\frac{1}{5}}=-4$ и $x^{-\frac{1}{5}}=3$.
Первое уравнение не имеет корней. Вспомним, что степенные функции с рациональным показателем определены только для положительных чисел.
Решим второе уравнение:
$x^{-\frac{1}{5}}=3$.
$\frac{1}{x^{\frac{1}{5}}}=3$.
$x^{\frac{1}{5}}=\frac{1}{3}$.
$\sqrt{x}=\frac{1}{3}$.
$x=(\frac{1}{3})^5=\frac{1}{243}$.

Ребята, мы рассмотрели два примера решения иррациональных уравнений.

Давайте перечислим основные методы решений иррациональных уравнений.
1) Возведение обеих частей уравнения в одну и ту же степень (при использовании этого метода нужно проверять полученные решения, так как могут возникнуть посторонние решения).
2) Метод замены переменных (введения новых переменных).
3) Построение графиков функций. Обе части уравнения представляем в виде функций, строим их графики и находим точки пересечения графиков.

Задачи для самостоятельного решения

1. Вычислить:
а) ${64}^{\frac{1}{3}}$.
б) ${64}^{\frac{5}{6}}$.
в) ${81}^{\frac{2}{3}}$.
г) ${(-317)}^{\frac{3}{7}}$.
2. Упростите выражение: $\frac{\sqrt{x}}{x^{\frac{1}{3}}-y^{\frac{1}{3}}}-\frac{\sqrt{y}}{x^{\frac{1}{3}}+y^{\frac{1}{3}}}$.
3. Решить уравнение:
а) $\sqrt{x^2}=8$.
б) $x^{\frac{2}{3}}=8$.
4. Решить уравнение: $x^{-\frac{2}{3}}-7x^{-\frac{1}{3}}+10=0$.

С любым целочисленным показателем, руководствуясь при этом следующими определениями:

Но математики на этом не остановились, они научились работать не только с целочисленными показателями. В этом параграфе мы обсудим, какой смысл придается в математике понятию степени с дробным показателем, т.е. выясним, что означают такие символы математического языка, как 2 5 , З -0"3 и т.д.

Зададимся вопросом: если вводить символ то каким математическим содержанием его наполнить? Хорошо бы, рассуждали математики, чтобы сохранялись привычные , например, чтобы при возведении степени в степень показатели перемножались, в частности, чтобы выполнялось следующее равенство:

Положим Тогда интересующее нас равенство можно переписать в виде а 5 =2 3 , откуда получаем Значит, появились основания определить

Подобные соображения и позволили математикам принять следующее определение.

Если

Самое любопытное, что введенное определение оказалось настолько удачным, что при нем сохранились все привычные свойства степеней, которые были доказаны для натуральных показателей: при умножении степеней с одинаковыми основаниями показатели складываются, при делении - вычитаются и т.д. Пусть, например, нам нужно выполнить умножение

Поскольку складывать дроби легче, чем применять свойства радикалов, на практике предпочитают заменять радикалы степенями с дробными показателями. Для иллюстрации этого положения вернемся к примеру Если перейти к дробным показателям, то получим:

Видите, насколько быстрее и проще мы получили здесь тот же результат, что и в § 42.
Пример 1. Вычислить:

г) Это задание некорректно, поскольку нет определения степени с дробным показателем для случая отрицательного основания. Математики договорились возводить в дробные степени только неотрицательные числа (и это оговорено в определении). Так что запись вида считается в математике лишенной смысла.
Замечание. Иногда приходится слышать возражения: неверно, что запись лишена смысла, ведь можно вычислить корень 3-й степени из числа -8; получится Так почему бы не считать, что

Если бы математики не запретили себе возводить в дробные степени отрицательные числа, то вот с какими неприятностями пришлось бы столкнуться:

Получилось «равенство» -2 = 2. Выбирая определения, математики как раз и заботятся о том, чтобы все было точно, определенно, недвусмысленно. Поэтому в определении степени с нулевым показателем а° появилось ограничение а в определении степени с положительным дробным показателем
Разумеется, математики не ограничились понятием степени с положительным дробным показателем, они ввели и определение степени с отрицательным дробным показателем, используя известную идею:

Но наличие дробного показателя заставляет сделать ограничение а>0, а наличие знаменателя заставляет сделать ограничение а= 0; в итоге приходится накладывать ограничение а > 0.

Если

Итак, теперь мы знаем, что такое степень с любым рациональным показателем. Справедливы следующие свойства (мы считаем, что а> 0, b> 0, s и t - произвольные рациональные числа):

Частичные обоснования указанных свойств были сделаны выше; этим мы и ограничимся.

Пример 2. Упростить выражение:

Пример 3. Решить уравнения:
а) Возведя обе части уравнения в куб, получаем:

х = ±1.
б) Это практически то же самое уравнение, что и в п. а), но с одной существенной оговоркой: поскольку переменная х возводится в дробную степень, она, по определению, должна принимать только неотрицательные значения. Значит, из найденных выше двух значений х в качестве корня уравнения мы имеем право взять лишь значение х = 1.
Ответ: а) ±1; б) 1.

Пример 4. Решить уравнение:
Введем новую переменную
Значит, получаем квадратное уравнение относительно новой переменной у:

у 2 -2у-8 = 0.

Решив это уравнение, получим: у 1 =-2, у 2 =4. Теперь задача сводится к решению двух уравнений:

Первое уравнение не имеет корней, поскольку (напомним еще раз) область допустимых значений для переменной х в подобных случаях определяется условием х > 0. Решая второе уравнение, последовательно находим:

Уравнения, в которых переменная содержится под знаком корня или возводится в дробную степень, называют иррациональными. Первое знакомство с иррациональными уравнениями состоялось у вас в курсе алгебры 8-го класса, где встречались уравнения, содержащие переменную под знаком квадратного корня. В этой главе мы рассмотрели еще несколько примеров решения иррациональных уравнений - пример 2 из § 39, пример 2 из § 40 и примеры 3 и 4 из § 43.

Основные методы решения иррациональных уравнений:

Метод возведения обеих частей уравнения в одну и ту же степень;
- метод введения новых переменных;
- функционально-графический метод.

Если используется метод возведения обеих частей уравнения в одну и ту же четную степень, то возможно появление посторонних корней, значит, обязательна проверка всех найденных решений - об этом мы говорили и раньше, в курсе алгебры 8-го класса.

А.Г. Мордкович Алгебра 10 класс

Содержание урока конспект урока опорный каркас презентация урока акселеративные методы интерактивные технологии Практика задачи и упражнения самопроверка практикумы, тренинги, кейсы, квесты домашние задания дискуссионные вопросы риторические вопросы от учеников Иллюстрации аудио-, видеоклипы и мультимедиа фотографии, картинки графики, таблицы, схемы юмор, анекдоты, приколы, комиксы притчи, поговорки, кроссворды, цитаты Дополнения рефераты статьи фишки для любознательных шпаргалки учебники основные и дополнительные словарь терминов прочие Совершенствование учебников и уроков исправление ошибок в учебнике обновление фрагмента в учебнике элементы новаторства на уроке замена устаревших знаний новыми Только для учителей идеальные уроки календарный план на год методические рекомендации программы обсуждения Интегрированные уроки

1. Одной из актуальных проблем современной методики преподавания в школе является развитие мотивации обучающихся. Увеличение умственной нагрузки на уроках математики заставляет задуматься над тем, как поддержать у учащихся интерес к изучаемому материалу, их активность на протяжении всего урока. Надо позаботиться о том, чтобы на уроках каждый ученик работал активно и увлечённо. В сложившейся ситуации на помощь учителю приходят игровые технологии – современный и признанный метод обучения и воспитания, обладающий образовательной, развивающей и воспитывающей функциями, которые действуют в органическом единстве. Игровые формы обучения на уроках математики дают возможность эффективной организации взаимодействия педагога и обучающихся. Даже самые пассивные учащиеся включаются в игру. Игровая деятельность мотивирует на обучение, в ходе игры каждый обучающийся получает возможность думать самостоятельно, развивать творческое мышление и решать разнообразные проблемы (то есть применять полученные знания в конкретной жизненной ситуации).

Скачать:

Предварительный просмотр:

Муниципальное бюджетное общеобразовательное учреждение средняя общеобразовательная школа № 24 с углублённым изучением отдельных предметов гуманитарного профиля им. И.С.Тургенева г. Орла

Методическая разработка урока

Алгебра и начала анализа

11 класс

Учебник: Мордкович А.Г. Алгебра и начала анализа. 10 -11 кл.: Учеб. Для общеобразоват. учреждений. – М.: Мнемозина, 2013. – 336с.:ил. (базовый)

Учитель математики: Морева Оксана Владимировна

Аннотация работы: Одной из актуальных проблем современной методики преподавания в школе является развитие мотивации обучающихся. Увеличение умственной нагрузки на уроках математики заставляет задуматься над тем, как поддержать у учащихся интерес к изучаемому материалу, их активность на протяжении всего урока. Надо позаботиться о том, чтобы на уроках каждый ученик работал активно и увлечённо. В сложившейся ситуации на помощь учителю приходят игровые технологии – современный и признанный метод обучения и воспитания, обладающий образовательной, развивающей и воспитывающей функциями, которые действуют в органическом единстве. Игровые формы обучения на уроках математики дают возможность эффективной организации взаимодействия педагога и обучающихся. Даже самые пассивные учащиеся включаются в игру. Игровая деятельность мотивирует на обучение, в ходе игры каждый обучающийся получает возможность думать самостоятельно, развивать творческое мышление и решать разнообразные проблемы (то есть применять полученные знания в конкретной жизненной ситуации).

Технологическая карта урока

	ФИО (полностью)		Морева Оксана Владимировна
	Место работы		МБОУ – СОШ № 24 с углублённым изучением отдельных предметов гуманитарного профиля им. И.С.Тургенева г. Орла
	Должность		Учитель
	Предмет		Алгебра и начала анализа
	Класс		11 класс
	Тема и номер урока в теме		Обобщение понятия о показателе степени (2 – ой урок)
	Базовый учебник		Мордкович А.Г. Алгебра и начала анализа. 10 -11 кл.: Учеб. Для общеобразоват. учреждений. – М.: Мнемозина, 2013. – 336с.: ил. (базовый)
	Цель урока		Выработать умение выполнять преобразование выражений, содержащих степени с дробным показателем
	Задачи	обучающие	Актуализация опорных знаний о степени с дробным показателем Отработка навыков преобразования выражений, содержащих степени с дробным показателем
		развивающие	Развитие: Операционного мышления, направленного на выбор оптимальных решений; Памяти и внимания; Умения применять полученные знания при решении задач.
		воспитательные	Формирование навыков групповой работы; Воспитание у обучающихся самостоятельности и ответственности за себя и других членов коллектива; Воспитание умения критически и объективно оценивать свою работу и работу товарища.
	Тип урока		Урок - деловая игра «Покорение вершины»
	Формы работы учащихся		Фронтальная, индивидуальная, групповая
	Необходимое техническое оборудование		Мультимедийный проектор и экран; Акустические колонки; Компьютеры.

План урока

1. Организационный момент (2-3 мин.)
2. Актуализация опорных знаний (5 мин.)
3. «Покорение вершин» (30 мин.)

• Первая высота (самопроверка)
• Вторая высота (групповая работа)
• Третья высота (индивидуальная дифференцированная работа).

1. Подведение итогов (4 - 5 мин.)
2. Домашнее задание (2 – 3 мин.)
3. Рефлексия достижения цели (1 мин.)

Ход урока:

1. Организационный момент

Урок начинается с прослушивания отрывка из песни В.В.Высоцкого «Лучше гор могут быть только горы» (слайд 2).

Учитель: У каждого в жизни есть вершины, которые они стремятся покорить. Кто – то хочет стать врачом, кто – то спортсменом, а кто – то может хочет стать альпинистом. Ведь высота всегда манила людей. Вспомните Икара, ведь его мечтой было полететь к Солнцу. И он осуществил свою мечту. Сущность человека состоит в том, чтобы всегда добиваться намеченной цели. Эпиграфом к нашему уроку подходят слова из прослушанной вами песни.

Как вечным огнем сверкает днем
Вершина изумрудным льдом,
Которую ты так и не покорил.

В.В.Высоцкий

Сегодня на уроке я приглашаю вас в экспедицию на покорение горных вершин. Вам предстоит перевоплотиться в спортсменов-альпинистов, покоряющих вершину знаний под названием «Степень с дробным показателем» (слайд 3).

Деятельность обучающихся: Обучающиеся записывают тему урока в рабочую тетрадь.

1. Актуализация опорных знаний

Учитель: Перед каждым из вас лежит карточка – счётчик, в которую вы будете заносить свои успехи в покорении горных вершин (приложение 1) . Впишите в верхнюю строку свои фамилию и имя. В этой карточке вы будете фиксировать прохождение каждой высоты в баллах. В конце урока вы самостоятельно подсчитаете набранные за урок баллы и выясните: удалось ли вам покорить “горную высоту» или нет.

Проверка снаряжения: “Что возьмем с собой в дорогу?” (слайд4).

Учитель: Как известно, экспедиции всегда предшествует тщательная подготовка, поэтому в начале, я предлагаю вам проверить свою готовность к покорению горной вершины.

1) Продолжите фразу: Если - обыкновенная дробь(q ≠1) и a ≥ 0, то под a p/q понимают…

2) Вычислите устно: 16 ¼ , 27 1/3 , 81 ¼ , 8 -1/3 , (-144) ½ (Задания можно заранее записать на доске или оформить в виде карточек)

3) Продолжите следующие свойства (Задания можно заранее записать на доске)

a s ∙ a t = …

a s : a t = …

(a s ) t = …

(ab) s = …

() s = …

4) Вычислите устно: (Задание можно заранее записать на доске)

Учитель: Итак, снаряжение собрано. Мы отправляемся в горы на покорение горных вершин.

1. Покорение вершин

Первая высота “Снежная лавина” (Самопроверка)

Учитель: Любые горы насколько прекрасны, настолько и опасны. В горах альпинистов поджидает множество опасностей. Первое, с чем нам придётся столкнуться в горах – это снежная лавина (слайд 5). Чтобы выбраться из – под снежного завала, необходимо выполнить следующее задание.

Деятельность обучающихся: Обучающиеся получает задание на два варианта и самостоятельно выполняют его в рабочих тетрадях. (Каждый ученик получает своё задание на карточке). Два ученика работают с обратной стороны доски. На выполнение задания отводится 5 – 7 минут.

Вариант 1

Вариант 2

1. Вычислите: 27 1/3 -25 -1/2 +16 3/4 -27 4/3
2. Упростите выражение: а) (125х -6 ) -2/3 ; б) (a∙a -1/3 ) 1/6 ∙a 8/9

По окончании работы обучающиеся, работавшие у доски, отворачивают доску. Их работу проверяет учитель. Обучающиеся, работавшие в тетрадях, осуществляют самопроверку. То есть каждый ученик самостоятельно проверяет правильность выполнения своего задания, опираясь на решение на доске. Каждое верно выполненное задание оценивается в 2 балла. Набранные баллы за прохождение «Снежной лавины» записываются в карточку-счетчик.

Физкультминутка.

Учитель: Покорение горных вершин дело очень трудное. Все мы очень устали освобождаясь из – под снежного завала. Предлагаю сделать привал.

Упражнение «А ну, попробуй!»:

Учитель предлагает учащимся вытянуть вперед руку раскрытой ладонью вверх. Прижмите к ладони большой палец. Остальные пальцы должны быть развернуты. А теперь прижмите мизинец. Получилось? Не тут-то было!

Вторая высота “Ледовая трещина” (работа в группах)

Учитель: Пока мы отдыхали, на нашем пути образовалась ледовая трещина (слайд 6). Знаете ли вы как альпинисты поступают в такой ситуации?

Примерные ответы обучающихся: Альпинисты помогают друг другу… Чтобы поднять альпиниста из трещины они бросают ему верёвку… Работают в связке…. Одному выбраться очень трудно, нужна помощь друга…….

Учитель: Из ваших ответов следует, чтобы выбраться из ледовой трещины, нужно работать в команде. Вот и мы с вами следующее задание будем выполнять в группах.

Деятельность обучающихся: Класс делится на группы по 4 – 5 человек. Каждая группа получает карточку с заданиями, в решении которых допущены ошибки. Обучающиеся должны их найти и исправить. На выполнение задания отводится 5 – 7 минут.

Карточка 1

Найдите ошибки

1. (121 1/2 +128 5/7 -81 5/4 )∙125 -1/3 = (11+32-81∙3)∙(-5) = -200∙(-5) = 1000
2. p-q = (p 2/3 -q 2/3 )(p 2/3 +2p 1/3 q 1/3 + q 2/3 )

Карточка 2

Найдите ошибки

Карточка 3

Найдите ошибки

1. (x 1/4 +1) (x 1/4 -1)(x 1/2 -1) = (x 1/4 -1) 2 (x 1/2 -1) = (x 1/2 -1)(x 1/2 -1) = (x 1/2 -1) 2
2. (-625) -1/4 = 625 1/4 = 5

Карточка 4

Найдите ошибки

По окончании работы, обучающие сообщают учителю найденные и исправленные ими ошибки. Учитель проверяет правильность выполнения задания. За каждую исправленную ошибку начисляется 2 балла каждому члену группы. Набранные баллы за прохождение «Ледовой трещины» записываются в карточку-счетчик.

Третья высота “Камнепад” (индивидуальная дифференцированная работа).

Учитель: Не успели мы выбраться из ледовой трещины, как на нас обрушился камнепад (слайд 7). Нужно расчистить завал. Все камни разные: большие и маленькие. Кто – то будет носить маленькие камни, а кто – то большие. Каждый выберет себе задание по силам.

Деятельность обучающихся: Обучающиеся получают на выбор дифференцированные задания различного уровня сложности.

Те, кто выбрали «большие камни», получают задания повышенного уровня на индивидуальных карточках. По результатам выполнения этого задания они смогут заработать до 8 баллов. Каждое верно выполненное задание оценивается в 2 балла.

Вариант 1

Сократите дробь:

а) ; b) ; c) ; d)

Вариант 2

Сократите дробь:

По окончании работы, учитель проверяет правильность выполнения задания.

А те, кто выбрал «маленькие камни», выполняют задания базового уровня в виде теста (см. интерактивный тест на диске или в приложении 2 ). По результатам выполнения этого задания они могут заработать до 5 баллов.

Набранные баллы за прохождение «Камнепада» записываются в карточку-счетчик.

1. Подведение итогов игры:

Учитель: Дорогие «альпинисты»! Давайте подсчитаем баллы, набранные вами по результатам трёх испытаний.

Деятельность обучающихся: Обучающиеся подсчитывают набранные ими баллы и записывают из в графе «Общий результат».

Учитель: Давайте подведём итоги (слайд 8). Если вы набрали 18-20 баллов, то вы покорили самую высокую вершину – молодцы (отметка отлично) ! Если вы набрали 15 – 17 баллов – покорили вторую высоту, хорошо (отметка хорошо) . Если 11 - 14 баллов –вы пока одолели только первую высоту, это тоже неплохо (отметка удовлетворительно) . Если вы набрали менее 11 баллов, то вы остались у подножия вершины. Но не огорчайтесь! Вам еще раз нужно пройти подготовку и повторить восхождение, ваша вершина у вас еще впереди!

Деятельность обучающихся: Обучающиеся согласно рейтингу выставляют себе отметку за урок в графе «Отметка» и сдают свою карточку – счётчик учителю.

Учитель (по своему усмотрению) переносит эти отметки в журнал.

1. Домашнее задание: § 37; № 37.28; № 37.30аг; № 37.39*б

№ 37.28. Сократите дробь: а) ; б) ; в) ; г) .

№ 37.30аг. Упростите выражение: а) (1 + ) 2 - 2 ; г) + - ( + ) 2

№ 37.39*б. Упростите выражение: б) ( + )

1. Рефлексия достижения цели:

Учитель: А теперь я попрошу вас продолжить одну или несколько фраз (слайд 9)

• было интересно…
• было трудно…
• я выполнял задания…
• у меня получилось …
• урок дал мне для жизни…

Деятельность обучающихся: Обучающиеся по желанию продолжают одну или несколько фраз.

Учитель: Наш урок начался с песни, а закончить его я хочу стихами (слайд 10) . Читает стихотворение.

Почетно стремление сердца к вершине,

Приятно на землю смотреть свысока.

Взошел... Ты герой, победитель отныне

И, кажется, мир поднебесный в руках.

Вершина – пустыня, лишь мудрые камни

Спокойно взирают сияние звёзд…

Для них ты никто, заблудившийся странник,

Иллюзии пленник, сомнительных грёз…

Вершина дает ощущенье полета,

Свободу от вечной мирской суеты,

Открыты к иному познанью ворота…

Волнительна зрелость ее чистоты…

Приложение к плану-конспекту урока «Обобщение понятия о показателе степени»

Приложение 1.

Карточка – счётчик __________________________ (Фамилия, имя)

Приложение 2.

Тест

Выберите один из предложенных ответов.

1. Упростите выражение: (1 – с 1/2 )(1 + с 1/2 )

• (1 – с 1/2 ) 2
• 1 – с
• 1 – 2с 1/2 + с

1. Упростите выражение: (1 – а 1/2 ) 2

• 1 – а + а 2

• – 2а + а 2

• 1 – 2а 1/2 + а

1. Разложите на множители: в 3/4 – в 1/2

• в 3/4 (1 – в)
• в 1/2 (в 1/4 – 1)
• в 1/2 (в 1/2 – 1)
• разложить нельзя

1. Разложите на множители: а – в

• ав (а 1/2 – в 1/2 )
• (а – в 1/2 )(а + в 1/2 )
• разложить нельзя
• (а 1/2 – в 1/2 ) (а 1/2 +в 1/2 )

Оценивание теста: 1 правильный ответ – 2 балла; 2 правильных ответа – 3 балла; 3 правильных ответа – 4 балла; 4 правильных ответа – 5 баллов.

Что умеете хорошего, то не забывайте, а чего не умеете, тому учитесь.
Из Владимира Мономаха.

Цели урока:

• Образовательная
  • систематизировать знания по пройденной теме;
  • проверить уровень изученного материала;
  • применить теоретический материал для решения задач.
• Воспитательная
  • воспитывать чувство ответственности за выполненную работу;
  • воспитывать культуру речи, аккуратность, внимание.
• Развивающие
  • развивать мыслительную деятельность учащихся;
  • прививать интерес к предмету;
  • развивать любознательность.

Урок повторения и обобщения материала.

Оборудование урока: кодоскоп таблицы.

Оформление урока: на доске тема урока, эпиграф.

Подготовка к уроку: за несколько дней на стенде вывешены вопросы для повторения.

• Определение степени с целым показателем
• Свойства степени с целым показателем.
• Определение степени с дробным показателем.
• Определение степени с дробным отрицательным показателем.
• Определение степени с любым показателем.
• Свойства степени с любым показателем.

Ход урока

1. Организационный момент.

2. Домашнее задание. № 1241, 1242, 1244а, 1245б.

3. Контроль домашнего задания.

Проводим взаимопроверку. Через кодоскоп показываю решения домашнего задания.

№1225б, в; 1227 а, в; 1229а,в;1232в,г;1233г.

Решение домашней работы.

Б) 2 1,3 * 2 -0,7 * 4 0,7 = 2 0,6 * (2 2) 0,7 =2 0,6 * 2 1,4 = 2 2 =4.

В) 49 -2\3 * 7 1\12 * 7 -3\4 = (7 2) -2\3 * 7 1\12 * 7 -3\4 = 7 -4\3 \+1\12 -3\4 = 7 (-16 +1- 9)\12 = 7 -24\12 = 7 -2 = 1\49.

А) (27 * 64) 1\3 = 27 1\3 * 64 1\3 = (3 3) 1\3 * (4 3) 1\3 = 3 * 4= 12.

В) (1\36 * 0,04) -1\2 = (6 -2 * (0,2) 2) -1\2 = (6 -2) -1\2 * ((0,2) 2) -1\2 = 6 * 0,2 -1 = 6 * 10\2=30.

А) = = х 1-3\5 = х 2\5 .

В) = = = с 8\3 -2\3 = с 2 .

В) (d 1\2 -1) * (d 1\2 +1)= d -1

Г) (p 1\3 - q 1\3) * (p 1\3 +(pq) 1\3 + q 2\3) = p- q.

Г) = = .

Рефлексия. Определяем количество ошибок.

4. Ориентация в изучаемом материале.

Ребята, какую тему мы изучали в течение нескольких последних уроков?

5. Мотивация. Сегодня мы проведём урок повторения и обобщения знаний по теме "Обобщение понятия степени". Ребята, обратите внимание на задания, которые мы будем решать на уроке, подобные им могут встречаться в контрольной работе, опросе.

6. Какими свойствами степеней вы пользовались при выполнении домашней работы? Вспомним теорию.

Дополните предложения:

7. Теоретически вы подковались, а теперь осталось проверить практическую часть.

Световой диктант.

(За закрытой доской 2 ученика.) Ребята выполняют задание через копирку, потом проверяем. Кодоскоп.

Вариант1	Вариант 2
Представьте выражение в виде степени с рациональным показателем.
; ; .	; ; .
Ответы. 2 1\2 ; х 2\3 ; а 4\5 .	16 1\5 ; 6 1\3 ; а 3\2 .
Представьте выражение в виде корня из числа или выражения
7 3\5 ; 5х 1\3 ; (5а) 1\3	5 -1\4 ; 7у 2\5 ; (6х) 2\5 .
Ответы. ; 5; .	; 7;
Вычислите
9 1\2 ; (3)	1. 16 1\2 (4)
8 2\3 (4)	2. 81 3\4 (27)
2 -2 * 16 1\2 (1)	3. 3 -2 * 81 1\4 (1\3).

8. А теперь послушаем кусочек истории. Историческая справка.

Представьте себе, что вы попали в Алмазный Фонд нашей страны. И вам побольше хотелось бы узнать об алмазах. Вот этим и займёмся на уроке.

Задание 1.

Выполните вычисления. Запишите в таблицы буквы, связанные с найденными ответами.

Б 49 1\2 = 7	Й 81 0,5 = 9
Ы 32 1\5 = 2	С 8 2\3 = 4
Е 1000 1\3 = 10	Н 0 0,2 = 0
П 0, 0016 1\4 = 0.2	Л 1 -0,6 = 1
И 16 - 1\2 = 0,25	З 16 -0,25 = 0,5
О (8\27) 1\3 = 2\3	Д 16 3\4 = 8
М (5 ) 0,25 = 1.5	А 25 1,5 =125

Название

что в переводе означает

0	10	0.2	2\3	7	10	8	0.25	1, 5	2	9
Н	Е	П	О	Б	Е	Д	И	М	Ы	Й

и отражает одно из его главных свойств - наивысшую твёрдость.

Задание 2.

Среди выражений, записанных в таблице, найдите и вычеркните те, которые не имеют смысла. Для остальных выражений найдите равные по значению числа, записанные на рисунках алмазов. Заполните свободные части таблицы числами и буквами.

Французское слово __brilliant_______________ (в русском написании __бриллиант______________________) в переводе означает "блестящий" и используется для обозначения алмазов, подвергнутых огранке и полировке. Такая обработка позволяет получить мистический блеск и великолепную игру света.

Задание 3.

А) Заполните таблицу

№	Выражение	Множество допустимых значений переменной	Слова
1.	Х 5		арена
6.	(-х) -5,1	(- ; 0)	площадка

Б) На рисунке показана совершенная бриллиантовая огранка, имеющая форму многогранника с 57 гранями. Эта оптимальная форма и размеры были получены в ХХ веке, благодаря развитию геометрической оптики.

Узнайте, как называются отдельные части такого бриллианта. Используя информацию из таблицы и рисунок:

Задание 4.

А) Упростите выражения:

Б) Найдите значения выражений

в) Используя найденные ответы, заполните пропуски в тексте. Слова пишите в нужных падежах.

Масса драгоценных камней измеряется каратами.: 1 карат = m 1 0,2 г.

Алмазы, имеющие массу более m 2 53 карат, получают собственные имена.

Наиболее крупные драгоценные камни хранятся в Алмазном фонде страны, расположенном в Московском Кремле.

Одним из самых знаменитых бриллиантов является алмаз

Затем попал в

В качестве выкупа за смерть

Он также был найден в

- "море света". Алмаз неоднократно похищался, попадал в различные страны и к разным правителям.

В 1773 году его приобрёл фаворит

Бриллиант был вставлен в Российский державный скипетр.

Задание 5.

А) Упростите выражения

Б) Выполните вычисления

1000 2\3 * 125 1\3 + (1\8) -4\3 + 16 0,25 * 49 0.5 = 530

В) Заполните пропуски в тексте:

Долгое время основным местом добычи алмазов была Индия, а в начале ХХ века были открыты месторождения в Южной Африке. Там в 1905 году на одном из приисков был найден крупнейший алмаз, масса которого составляла 3106 карат. Он был назван именем хозяина прииска.

Куллинан 11 - вторая по величине часть, полученная при гранении алмаза, украсил корону королевы Виктории.

При огранке этот алмаз был рассечён на 9 частей. Наибольшая часть, имеющая массу 530 карат, была названа "Звезда Африки". Этот бриллиант, имеющий 74 грани, стал украшать британский державный скипетр.

Подводим итог урока.

1. Какую цель ставили в начале урока?
2. Достигли ли цели урока?
3. Что нового узнали на уроке?
4. Ставим оценки за урок.